Calcul de puissances non-entières
Page 1 sur 1
Calcul de puissances non-entières
par mi_li_mi Lun 5 Déc 2011 - 15:48
Réponse à la queston de porteuris, à propos du calcul de puissances non-entières:
Bonjour Porteuris
Je prends un exemple : calcul de 3^0,3 soit 3^3/10
3^0,3 = 3^(0,1 + 0,1 + 0,1) = 3^0,1 . 3^0,1 .3^0,1 = (3^0,1)^3
[ a^(n + p) = (a^n) . (a^p) ] et [ (a^n)^p = a^(n . p) ]
On calcule d'abord 3^0,1 soit 3^1/10
3^1/10 = 10ème de 3 = x , soit : x^10 = 3
Par encadrements suuccessifs tu calcules x (extraction de la 10ème de 3) :
1^10 < x^10 < 2^10
1,1^10 < x^10 < 1,2^10
1,11^10 < x^10 < 1,12^10
1,116^10 < x^10 < 1,17 ^10
Evidemment à la main, pour trouver les encadrements, c'est long, il faut effectuer :
1,11 . 1,11 . 1,11 . ... . 1,11 dix fois à la main et ainsi pour les autres valeurs ( je vous avoue que pour trouver les encadrements, j'ai utilisé une calcularice mais on peut le faire à la main, ce sera plus long c'est tout)
soit x = 3^1/10 = 3^0,1 = 1,116 à 0,001 près par défaut.
NOTE : En utilisant les propriétés des puissances, on peut réduire le nombre d'opérations, pour calculer a^10,
au lieu de faire : a . a . a . ... .a (10 fois), ce qui ferait 9 opérations,
on calculera :
a . a = a^2 : 1 opération
a^2 . a^2 = a^4 : 1 op.
a^4 . a^4 = a^8 : 1 op.
a^8 . a^2 = a^10 : 1 op.
Total : 4 opérations
Il faudra donc 4 opérations au lieu de 9 pour calculer 1,11^10 par exemple (ce qui est appréciable si on calcule à la main).
Maintenant calculons : 3^0,3
3^0,3 = 3^3/10 = 3^(1/10 + 1/10 + 1/10) = 3^1/10 . 3^1/10 . 3^1/10
On obtient : 3^0.3 = (3^1/10)^3
3^0,3 = (1,116)^3
3^0,3 = 1,389 (en utilisant x = 1,116 à 0,001 près par défaut, c'est à dire trois chiffres après la virgule)
La valeur à la calcularice est : 1,39038917
Le calcul est précis à 0,01 près par défaut, c'est à dire qu'il est parfaitement fiable jusqu'au premier chiffre après la virgule compris.
AUTRE EXEMPLE :
Calculons 4^2,6 :
4^2,6 = 4^(2+0,6) 4^(2+ 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1)
4^2,6 = 4^2 . 4^0,1 . 4^0,1 . 4^0,1 . 4^0,1 . 4^0,1 .4^0,1
4^2,6 = 4^2 . (4^0,1)^6
4^0,1 = 4^1/10 = 10ème de 4 = x , soit x^10 = 4
Calcul par encadrements successifs de la valeur de x (extraction de la 10ème de 4) :
1^10 < x^10<2^10
1,1^10< x^10 < 1,2^10
1,1^10 < x^10 < 1,15^10
1,148^0 < x^10 <1,149^10
1,1486^10 < x^10 < 1,1487^10
1,14869^10 < x^10 <1,14870^10
Soit : 4^0,1 = 4^1/10 = 1,14869à 0,000 01 près par défaut.
Plus on resserre l'encadrement (ici, cinq chiffres après la virgule) plus le résultat final sera précis.
4^2,6 = 4^2 . (4^1/10)^6
4^2,6 = 4^2 . (1,14869)^6
4^2,6 = 16 . 1,14869 . 1,14869 . ... . 1,14869 (six fois)
4^2,6 = 36,75674 (en utilisant x = 1,14869 à 0,000 01 près par défaut.
La calculatrice donne : 4^2,6 = 36,75834736
Le calcul est donc précis à 0,001 près par défaut, il est donc parfaitement exact jusqu'au 2ème chiffre après la virgule compris.
En continuant les encadrements jusqu'à 7 chiffres après la virgule :
1,148698^10 < x^10 < 1,148699^10
1,1486983^10 < x^10 < 1,1486984^10
Si on prend x = 1,186983 à 0,000 000 1 près par défaut, on obtient 4^2,6 = 36,75833
Résultat calculatrice : 36,75834736
Le calcul est précis à 0,000 01 près par défaut,il est fiable jusqu'au 4ème chiffre après la virgule compris.
On poursuit encore les encadrements jusqu'à 9 chiffres après la virgule :
1,148 698 35^10 < x^10 < 1,148 698 36^10
1,148 698 354^^10 < x^10 1,148 698 355^0 (voir * plus bas)
Si on prend x = 1,148 698 354 à 0,000 000 001 près par défaut,
on obtient : 4^2,6 = 36,758 347 17
Résultat calculatrice : 4^2,6 = 36,758 347 36
Le calcul est précis à 0,000 000 1 pès par défaut, il est donc parfaitement juste jusqu'au 6 ème chiffre après la virgule compris.
* 1,148 698 355 est la valeur exacte de x : (1,148 698 355)^10 = 4 et 10ème de 4 = 1,148 698 355
ENCORE UN EXEMPLE ( avec une puissance non-entière à 2 chiffres après la virgule) :
Calculons 7^3,46 :
7^3,46 = 7^(3 + 0,4 + 0,06)
7^3,46 = 7^(3 + 0,1 + 0,1 + 0,1 + 0,1 + 0,01 +0,01 + 0,01 + 0,01 + 0,01 + 0,01)
7^3,46 = 7^3 . 7^0,1 . 7^0,1 . 7^0,1 . 7^0,1 . 7^0,01 7^0,01 . 7^0,01 . 7^0,01 . 7^0,01 . 7^0,01
7^3,46 = 7^3 . (7^0,1)^4 . (7^0,01)^6
Calcul de 7^0,1 soit 7^1/10 :
7^0,1 = 7^1/10 = 10ème de 7 = x , soit : x^10 = 7
Calcul par encadrements successif de la valeur de x (extraction de la 10ème de 7) :
1^10 < x ^10 < 2^10
1,2^10 < x^10 < 1,3^10
1,21 ^10 < x^10 < 1,22^10
1,214^10 < x^10 < 1,215^10
1,2148^10 < x^10 < 1,2149^10
1,21481^10 < x^10 < 1,21482^10
1,214814^10 < x^10 < 1,214815^10
On obtient : x = 7^0,1 = 1,214814 à 0,000 001 près par défaut
Calcul de 7^0,01 soit 7^1/100 :
7^0,01 = 7^1/100 = 100ème de 7 = y soit y^100 = 7
Calcul de la valeur de y par encadrement successif (ou extraction de la 100ème de 7) :
1^100 < y^100 < 2^100
1,01^100 < y^100 < 1,02^100
1,019^100 < y^100 < 1,020^100
1,019 6^100 < y^100 < 1,019 7^100
1,019 64^100 < y^100 < 1,019 65^100
1,019 649^100 < y^100 < 1,019 650^100
On trouve : y = 7^0,01 = 1,019 649 à 0,000 001 près par défaut
pour extraire la 100ème de 7 à la main, si on doit (sans se tromper) multiplier :
1,019 649 . 1,019649 . ... . 1,019649 (100 fois) pour s'assurer que 1,019649^100 ne dépasse pas 7, il faut avoir plusieurs
années devant soi :-) et essayez d'imaginer pour extraire la 1000ème.
NOTE : Comme précédemment, on peut réduire le nombre d'opérations pour calculer a^100 ou a^1000 :
I) si on calcule a . a . a . a . ... .a (100 fois), cela fait 99 opérations,
on calculera :
a . a = a^2 : 1 opération
a^2 . a^2 = a^4 : 1 op.
a^4 . a^4 = a^8 : 1 op.
a^8 . a^8 = a^16 : 1 op.
a^16 . a^16 = a^32 : 1 op.
a^32 . a^32 = a^64 : 1 op.
a^64 . a^32 = a^96 : 1 op.
a^96 . a^4 = a^100 : 1 op. (a^4 a été calculé plus haut)
Total : 8 opérations
On obtient 8 opérations au lieu de 99 pour calculer 1,019649^100, par exemple, à la main.
II) Pour calculer a^1000 = a . a . a . a . ... . a (1000fois), il faut 999 opérations, bon courage !
On reprend le calcul précédent de a^100 :
a^100 : 8 opérations
a^100 . a^100 = a^200 : 1 op.
a^200 . a^200 = a^400 : 1 op.
a^400 . a^400 = a^800 : 1 op.
a^800 . a^200 = a^1000 : 1 op. (a^200 a été calculé plus haut)
Total : 12 opérations
Il faudra donc 12 opérations pour calculer, par exemple, 1,1^1000 à la main, c'est encore long mais quand même
bien moins que 999 opérations.
III) Pour calculer a^10000, il faudra faire 4 opérations supplémentaires :
on reprend le calcul de a^1000 ( 12 opérations) et on rajoute :
a^1000 . a^1000 = a^2000
a^2000 . a^2000 = a^4000
a^4000 . a^4000 = a^8000
A^8000 . a^2000 = a^10000 (a^2000 a été calculé plus haut),
16 opérations en tout au lieu de 9999 si on fait : a . a . a . ... . a(10000 fois).
Calcul de 7^3,46 :
7^3,46 = 7^3 . (7^0,1)^4 . (7^0,01)^6
7^3,46 = 7^3 . (1,214 814)^4 . (1,019 649)^6
7^3,46 = 343 . 2,177 906 . 1,123 839
7^3,46 = 839,53 2 185 (en utilisant x = 1,214 814 et y = 1,019 649 à 0,000 001 près par défaut)
Résultat de la calculatrice : 7^3,46 = 839,53 5 796 4
On obtient un résultat précis à 0,001 près par défaut et le calcul est parfaitement fiable jusqu'au 2ème chiffre après la virgule compris.
On peut continuer ainsi avec des puissances à 3 , 4 chiffres après la virgule ou plus, il suffira d'extraire la 1000ème,
10 000ème, 100 000ème etc. du nombre qu'on a élevé à la puissance en question.
ADDENDUM :
Pour calculer les puissances non-entières, on peut aussi lorsque c'est utile se servir de la racine carrée :
en effet : a = a^0,5 = a^1/2.
Ce procédé est surtout intéressant si on connaît la racine carrée du nombre élevé à la puissance non-entière, autrement il faudra l'extraire par le même moyen qu'on utilise pour calculer la racine dixième, c'est un travail supplémentaire.
I) Si l'on reprend le 1er exemple :
3^0,3 = 3^(0,5 - 0,2)
3^0,3 = (3^0,5) / (3^0,2) [ a^(n - p) = (a^n) / (a^p) ]
3^0,3 = ( :sqrt:3) / ( dixième de 3)^2
Dans ce cas-ci, ce procédé n'est pas très intéressant.
II) Si on reprend le 2ème exemple :
4^2,6 = 4^2 . 4^0,5 . 4^0,1
4^2,6 = 4^2 . ( 4) . ( 10ème de 4)
4^2,6 = 16 . 2 . ( 10ème de 4)
4^2,6 = 32 . ( 10ème de 4)
Ici, le procédé est utile, à la main, il ne faut plus qu'une seule opération pour calculer 4^2,6.
On peut aussi poser :
4^2,6 = 4^(3 - 0,4)
4^2,6 = (4^3) / (4^0,4)
4^2,6 = (4^3) / ( 10ème de 4)^4
Dans ce cas, il faut aimer faire les divisions euclidiennes à la main.
III) Prenons 4^2,61 :
4^2,61 = 4^(2 + 0,5 +0,1 + 0,01)
= 4^2 . 4^0,5 . 4^0,1 . 4^0,01
= 4^2 . ( :sqrt:4) . ( 10ème de 4) . ( 100ème de 4)
= 16 . 2 . ( 10ème de 4) . ( 100ème de 4)
= 32 . ( 10 ème de 4) . ( 100ème de4)
ou
4^2,61 = 4^(3 - 0,39)
4^2,61 = (4^3) / (4^0,39)
4^2,61 = 4^3 . / [4^(0,3 + 0,09)]
4^2,61 = 4^3 / (4^0,3 . 4^0,09)
4^2,61 = 64 / [( 10ème de 4)^3 . ( 100ème de 4)^9]
IV) Prenons 4^(-2,61) :
4^(-2,61) = 4^(-2 - 0,5 - 0, 1- 0,01)
4^(-2,61) = 4^-2 . 4^-0,5 . 4^-0,1 . 4^-0,01
4^(-2,61) = 1 / (4^2 . 4^0,5 . 4^0,1 . 4^0,01)
4^(-2,61) = 1 / [4^2 . ( 4) . ( 10ème de 4) . ( 100ème de 4)]
4^(-2,61) = 1 / [ 16 . 2 . ( 10ème de 4) . ( 100ème de 4)]
4^(-2,61) = 1 / [32 . ( 10ème de ) . ( 100ème de 4)]
4^(-2,61) = 1 / (4^2,61)
ou 4^(-2,61) = 4^(-3 + 0,39)
4^(-2,61) = 4^-3 . 4^0,3 . 4^0,09
4^(-2,61) = (1 / 4^3) . (4^0,1)^3 . (4^0,01)^9
4^(-2,61) = [( 10ème de 4)^3 . ( 100ème de 4)^9] / 4^3
4^(-2,61) = [( 10ème de 4)^3 . ( 100ème de 4)^9] / 64
4^(-2,61) = 1 / 4^2,61 = 1 / 4^(3-0,39)
V) On peut retenir que : avec n ,
(n,5) 0
a^n,5 = a^(n + 0,5)
a^n,5 = (a^n) . ( a)
(-n,5) 0
a^(-n,5) = a(-n - 0,5)
a^(-n,5) = a^(-n) . a^(-0,5) [ a^(-n) = (a^n)^-1 = 1 / (a^n) ]
a^(-n,5) = (1 / a^n) . (1 / a^0,5)
a^(-n,5) = 1 /[(a^n) . ( a)]
Avec n
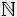*, soit n 
0 :
a^(1/n) =
énième de a
a^(1/-n) 1/ énième de a
ainsi par exemple :
a^(1/2) = a et
a^(1/23) = 23ième de a
a^(1/-2) = 1/ a
a^(1/-23) = 1/ 23ième de a
Exemples :
1) 4^2,5 = (4^2) . (4^0,5)
4^2,5 = (4^2) . 4
4^2,5 = 16 . 2
4^2,5 = 32
1') autre méthode :
4^2,5 = 4^(3-0,5)
4^2,5 = (4^3) / (4^0,5)
4^2,5 = 64 / 4
4^2,5 = 64 / 2
4^2,5 = 32
2) 4^(-2,5) = 4^(-2-0,5)
4^(-2,5) = 4^(-2) . 4^(-0,5)
4^(-2,5) = (1 / 4^2) . (1 / 4^0,5)
4^(-2,5) = 1 / (4^2 . 4^0,5)
4^(-2,5) = 1 /(16 . 4)
4^(-2,5) = 1 / (16 . 2)
4^(-2,5) = 1 /32
2') Autre méthode :
4^(-2,5) = 4^(-3 + 0,5)
4^(-2,5) = 4^(-3) . 4^0;5
4^(-2,5) = (1 / 4^3) . ( 4)
4^(-2,5) = 2 / 64
4^(-2,5) = 1 / 32
A la main, jusqu'à une puissance avec 1 chiffre après la virgule ça va, à partir de 2 chiffres, c'est quand même long et il faut être sûr de vivre vieux :-) .
J'espère que cela vous aidera,
bonne journée.
mi_li_mi
Bonjour Porteuris
Je prends un exemple : calcul de 3^0,3 soit 3^3/10
3^0,3 = 3^(0,1 + 0,1 + 0,1) = 3^0,1 . 3^0,1 .3^0,1 = (3^0,1)^3
[ a^(n + p) = (a^n) . (a^p) ] et [ (a^n)^p = a^(n . p) ]
On calcule d'abord 3^0,1 soit 3^1/10
3^1/10 = 10ème de 3 = x , soit : x^10 = 3
Par encadrements suuccessifs tu calcules x (extraction de la 10ème de 3) :
1^10 < x^10 < 2^10
1,1^10 < x^10 < 1,2^10
1,11^10 < x^10 < 1,12^10
1,116^10 < x^10 < 1,17 ^10
Evidemment à la main, pour trouver les encadrements, c'est long, il faut effectuer :
1,11 . 1,11 . 1,11 . ... . 1,11 dix fois à la main et ainsi pour les autres valeurs ( je vous avoue que pour trouver les encadrements, j'ai utilisé une calcularice mais on peut le faire à la main, ce sera plus long c'est tout)
soit x = 3^1/10 = 3^0,1 = 1,116 à 0,001 près par défaut.
NOTE : En utilisant les propriétés des puissances, on peut réduire le nombre d'opérations, pour calculer a^10,
au lieu de faire : a . a . a . ... .a (10 fois), ce qui ferait 9 opérations,
on calculera :
a . a = a^2 : 1 opération
a^2 . a^2 = a^4 : 1 op.
a^4 . a^4 = a^8 : 1 op.
a^8 . a^2 = a^10 : 1 op.
Total : 4 opérations
Il faudra donc 4 opérations au lieu de 9 pour calculer 1,11^10 par exemple (ce qui est appréciable si on calcule à la main).
Maintenant calculons : 3^0,3
3^0,3 = 3^3/10 = 3^(1/10 + 1/10 + 1/10) = 3^1/10 . 3^1/10 . 3^1/10
On obtient : 3^0.3 = (3^1/10)^3
3^0,3 = (1,116)^3
3^0,3 = 1,389 (en utilisant x = 1,116 à 0,001 près par défaut, c'est à dire trois chiffres après la virgule)
La valeur à la calcularice est : 1,39038917
Le calcul est précis à 0,01 près par défaut, c'est à dire qu'il est parfaitement fiable jusqu'au premier chiffre après la virgule compris.
AUTRE EXEMPLE :
Calculons 4^2,6 :
4^2,6 = 4^(2+0,6) 4^(2+ 0,1 + 0,1 + 0,1 + 0,1 + 0,1 + 0,1)
4^2,6 = 4^2 . 4^0,1 . 4^0,1 . 4^0,1 . 4^0,1 . 4^0,1 .4^0,1
4^2,6 = 4^2 . (4^0,1)^6
4^0,1 = 4^1/10 = 10ème de 4 = x , soit x^10 = 4
Calcul par encadrements successifs de la valeur de x (extraction de la 10ème de 4) :
1^10 < x^10<2^10
1,1^10< x^10 < 1,2^10
1,1^10 < x^10 < 1,15^10
1,148^0 < x^10 <1,149^10
1,1486^10 < x^10 < 1,1487^10
1,14869^10 < x^10 <1,14870^10
Soit : 4^0,1 = 4^1/10 = 1,14869à 0,000 01 près par défaut.
Plus on resserre l'encadrement (ici, cinq chiffres après la virgule) plus le résultat final sera précis.
4^2,6 = 4^2 . (4^1/10)^6
4^2,6 = 4^2 . (1,14869)^6
4^2,6 = 16 . 1,14869 . 1,14869 . ... . 1,14869 (six fois)
4^2,6 = 36,75674 (en utilisant x = 1,14869 à 0,000 01 près par défaut.
La calculatrice donne : 4^2,6 = 36,75834736
Le calcul est donc précis à 0,001 près par défaut, il est donc parfaitement exact jusqu'au 2ème chiffre après la virgule compris.
En continuant les encadrements jusqu'à 7 chiffres après la virgule :
1,148698^10 < x^10 < 1,148699^10
1,1486983^10 < x^10 < 1,1486984^10
Si on prend x = 1,186983 à 0,000 000 1 près par défaut, on obtient 4^2,6 = 36,75833
Résultat calculatrice : 36,75834736
Le calcul est précis à 0,000 01 près par défaut,il est fiable jusqu'au 4ème chiffre après la virgule compris.
On poursuit encore les encadrements jusqu'à 9 chiffres après la virgule :
1,148 698 35^10 < x^10 < 1,148 698 36^10
1,148 698 354^^10 < x^10 1,148 698 355^0 (voir * plus bas)
Si on prend x = 1,148 698 354 à 0,000 000 001 près par défaut,
on obtient : 4^2,6 = 36,758 347 17
Résultat calculatrice : 4^2,6 = 36,758 347 36
Le calcul est précis à 0,000 000 1 pès par défaut, il est donc parfaitement juste jusqu'au 6 ème chiffre après la virgule compris.
* 1,148 698 355 est la valeur exacte de x : (1,148 698 355)^10 = 4 et 10ème de 4 = 1,148 698 355
ENCORE UN EXEMPLE ( avec une puissance non-entière à 2 chiffres après la virgule) :
Calculons 7^3,46 :
7^3,46 = 7^(3 + 0,4 + 0,06)
7^3,46 = 7^(3 + 0,1 + 0,1 + 0,1 + 0,1 + 0,01 +0,01 + 0,01 + 0,01 + 0,01 + 0,01)
7^3,46 = 7^3 . 7^0,1 . 7^0,1 . 7^0,1 . 7^0,1 . 7^0,01 7^0,01 . 7^0,01 . 7^0,01 . 7^0,01 . 7^0,01
7^3,46 = 7^3 . (7^0,1)^4 . (7^0,01)^6
Calcul de 7^0,1 soit 7^1/10 :
7^0,1 = 7^1/10 = 10ème de 7 = x , soit : x^10 = 7
Calcul par encadrements successif de la valeur de x (extraction de la 10ème de 7) :
1^10 < x ^10 < 2^10
1,2^10 < x^10 < 1,3^10
1,21 ^10 < x^10 < 1,22^10
1,214^10 < x^10 < 1,215^10
1,2148^10 < x^10 < 1,2149^10
1,21481^10 < x^10 < 1,21482^10
1,214814^10 < x^10 < 1,214815^10
On obtient : x = 7^0,1 = 1,214814 à 0,000 001 près par défaut
Calcul de 7^0,01 soit 7^1/100 :
7^0,01 = 7^1/100 = 100ème de 7 = y soit y^100 = 7
Calcul de la valeur de y par encadrement successif (ou extraction de la 100ème de 7) :
1^100 < y^100 < 2^100
1,01^100 < y^100 < 1,02^100
1,019^100 < y^100 < 1,020^100
1,019 6^100 < y^100 < 1,019 7^100
1,019 64^100 < y^100 < 1,019 65^100
1,019 649^100 < y^100 < 1,019 650^100
On trouve : y = 7^0,01 = 1,019 649 à 0,000 001 près par défaut
pour extraire la 100ème de 7 à la main, si on doit (sans se tromper) multiplier :
1,019 649 . 1,019649 . ... . 1,019649 (100 fois) pour s'assurer que 1,019649^100 ne dépasse pas 7, il faut avoir plusieurs
années devant soi :-) et essayez d'imaginer pour extraire la 1000ème.
NOTE : Comme précédemment, on peut réduire le nombre d'opérations pour calculer a^100 ou a^1000 :
I) si on calcule a . a . a . a . ... .a (100 fois), cela fait 99 opérations,
on calculera :
a . a = a^2 : 1 opération
a^2 . a^2 = a^4 : 1 op.
a^4 . a^4 = a^8 : 1 op.
a^8 . a^8 = a^16 : 1 op.
a^16 . a^16 = a^32 : 1 op.
a^32 . a^32 = a^64 : 1 op.
a^64 . a^32 = a^96 : 1 op.
a^96 . a^4 = a^100 : 1 op. (a^4 a été calculé plus haut)
Total : 8 opérations
On obtient 8 opérations au lieu de 99 pour calculer 1,019649^100, par exemple, à la main.
II) Pour calculer a^1000 = a . a . a . a . ... . a (1000fois), il faut 999 opérations, bon courage !
On reprend le calcul précédent de a^100 :
a^100 : 8 opérations
a^100 . a^100 = a^200 : 1 op.
a^200 . a^200 = a^400 : 1 op.
a^400 . a^400 = a^800 : 1 op.
a^800 . a^200 = a^1000 : 1 op. (a^200 a été calculé plus haut)
Total : 12 opérations
Il faudra donc 12 opérations pour calculer, par exemple, 1,1^1000 à la main, c'est encore long mais quand même
bien moins que 999 opérations.
III) Pour calculer a^10000, il faudra faire 4 opérations supplémentaires :
on reprend le calcul de a^1000 ( 12 opérations) et on rajoute :
a^1000 . a^1000 = a^2000
a^2000 . a^2000 = a^4000
a^4000 . a^4000 = a^8000
A^8000 . a^2000 = a^10000 (a^2000 a été calculé plus haut),
16 opérations en tout au lieu de 9999 si on fait : a . a . a . ... . a(10000 fois).
Calcul de 7^3,46 :
7^3,46 = 7^3 . (7^0,1)^4 . (7^0,01)^6
7^3,46 = 7^3 . (1,214 814)^4 . (1,019 649)^6
7^3,46 = 343 . 2,177 906 . 1,123 839
7^3,46 = 839,53 2 185 (en utilisant x = 1,214 814 et y = 1,019 649 à 0,000 001 près par défaut)
Résultat de la calculatrice : 7^3,46 = 839,53 5 796 4
On obtient un résultat précis à 0,001 près par défaut et le calcul est parfaitement fiable jusqu'au 2ème chiffre après la virgule compris.
On peut continuer ainsi avec des puissances à 3 , 4 chiffres après la virgule ou plus, il suffira d'extraire la 1000ème,
10 000ème, 100 000ème etc. du nombre qu'on a élevé à la puissance en question.
ADDENDUM :
Pour calculer les puissances non-entières, on peut aussi lorsque c'est utile se servir de la racine carrée :
en effet : a = a^0,5 = a^1/2.
Ce procédé est surtout intéressant si on connaît la racine carrée du nombre élevé à la puissance non-entière, autrement il faudra l'extraire par le même moyen qu'on utilise pour calculer la racine dixième, c'est un travail supplémentaire.
I) Si l'on reprend le 1er exemple :
3^0,3 = 3^(0,5 - 0,2)
3^0,3 = (3^0,5) / (3^0,2) [ a^(n - p) = (a^n) / (a^p) ]
3^0,3 = ( :sqrt:3) / ( dixième de 3)^2
Dans ce cas-ci, ce procédé n'est pas très intéressant.
II) Si on reprend le 2ème exemple :
4^2,6 = 4^2 . 4^0,5 . 4^0,1
4^2,6 = 4^2 . ( 4) . ( 10ème de 4)
4^2,6 = 16 . 2 . ( 10ème de 4)
4^2,6 = 32 . ( 10ème de 4)
Ici, le procédé est utile, à la main, il ne faut plus qu'une seule opération pour calculer 4^2,6.
On peut aussi poser :
4^2,6 = 4^(3 - 0,4)
4^2,6 = (4^3) / (4^0,4)
4^2,6 = (4^3) / ( 10ème de 4)^4
Dans ce cas, il faut aimer faire les divisions euclidiennes à la main.
III) Prenons 4^2,61 :
4^2,61 = 4^(2 + 0,5 +0,1 + 0,01)
= 4^2 . 4^0,5 . 4^0,1 . 4^0,01
= 4^2 . ( :sqrt:4) . ( 10ème de 4) . ( 100ème de 4)
= 16 . 2 . ( 10ème de 4) . ( 100ème de 4)
= 32 . ( 10 ème de 4) . ( 100ème de4)
ou
4^2,61 = 4^(3 - 0,39)
4^2,61 = (4^3) / (4^0,39)
4^2,61 = 4^3 . / [4^(0,3 + 0,09)]
4^2,61 = 4^3 / (4^0,3 . 4^0,09)
4^2,61 = 64 / [( 10ème de 4)^3 . ( 100ème de 4)^9]
IV) Prenons 4^(-2,61) :
4^(-2,61) = 4^(-2 - 0,5 - 0, 1- 0,01)
4^(-2,61) = 4^-2 . 4^-0,5 . 4^-0,1 . 4^-0,01
4^(-2,61) = 1 / (4^2 . 4^0,5 . 4^0,1 . 4^0,01)
4^(-2,61) = 1 / [4^2 . ( 4) . ( 10ème de 4) . ( 100ème de 4)]
4^(-2,61) = 1 / [ 16 . 2 . ( 10ème de 4) . ( 100ème de 4)]
4^(-2,61) = 1 / [32 . ( 10ème de ) . ( 100ème de 4)]
4^(-2,61) = 1 / (4^2,61)
ou 4^(-2,61) = 4^(-3 + 0,39)
4^(-2,61) = 4^-3 . 4^0,3 . 4^0,09
4^(-2,61) = (1 / 4^3) . (4^0,1)^3 . (4^0,01)^9
4^(-2,61) = [( 10ème de 4)^3 . ( 100ème de 4)^9] / 4^3
4^(-2,61) = [( 10ème de 4)^3 . ( 100ème de 4)^9] / 64
4^(-2,61) = 1 / 4^2,61 = 1 / 4^(3-0,39)
V) On peut retenir que : avec n ,
(n,5) 0
a^n,5 = a^(n + 0,5)
a^n,5 = (a^n) . ( a)
(-n,5) 0
a^(-n,5) = a(-n - 0,5)
a^(-n,5) = a^(-n) . a^(-0,5) [ a^(-n) = (a^n)^-1 = 1 / (a^n) ]
a^(-n,5) = (1 / a^n) . (1 / a^0,5)
a^(-n,5) = 1 /[(a^n) . ( a)]
Avec n
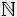*, soit n 0 :a^(1/n) =
énième de a a^(1/-n) 1/
énième de aainsi par exemple :
a^(1/2) =
a eta^(1/23) =
23ième de aa^(1/-2) = 1/
aa^(1/-23) = 1/
23ième de aExemples :
1) 4^2,5 = (4^2) . (4^0,5)
4^2,5 = (4^2) . 4
4^2,5 = 16 . 2
4^2,5 = 32
1') autre méthode :
4^2,5 = 4^(3-0,5)
4^2,5 = (4^3) / (4^0,5)
4^2,5 = 64 / 4
4^2,5 = 64 / 2
4^2,5 = 32
2) 4^(-2,5) = 4^(-2-0,5)
4^(-2,5) = 4^(-2) . 4^(-0,5)
4^(-2,5) = (1 / 4^2) . (1 / 4^0,5)
4^(-2,5) = 1 / (4^2 . 4^0,5)
4^(-2,5) = 1 /(16 . 4)
4^(-2,5) = 1 / (16 . 2)
4^(-2,5) = 1 /32
2') Autre méthode :
4^(-2,5) = 4^(-3 + 0,5)
4^(-2,5) = 4^(-3) . 4^0;5
4^(-2,5) = (1 / 4^3) . ( 4)
4^(-2,5) = 2 / 64
4^(-2,5) = 1 / 32
A la main, jusqu'à une puissance avec 1 chiffre après la virgule ça va, à partir de 2 chiffres, c'est quand même long et il faut être sûr de vivre vieux :-) .
J'espère que cela vous aidera,
bonne journée.
mi_li_mi
mi_li_mi- Membre
-
Nombre de messages : 11
Age : 64
Localisation : France
Profession / Etudes : Maths-Physique
Points : 4829
Date d'inscription : 28/11/2011
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
» Devoir maison sur équilibre et réaction chimique
» Ma présentation
» projet scientique sur la LUMIERE
» La trajectoire de la Terre
» Equilibrer une réaction redox
» les effets sur les lignes de transport de l’électricité
» lignes de transport de l'électricité
» Gravitation
» Maquette suspension de moto 2D