Les problèmes d'Ephemere
2 participants
Page 1 sur 1
 Les problèmes d'Ephemere
Les problèmes d'Ephemere
Bon, je propose de mettre 5 problèmes chaque dimanche avant midi, du moins quand j'en ai la possibilité.
Il n'est pas nécessaire de répondre à chaque problème pour m'envoyer une solution. On peut même me renvoyer la solution d'un seul et unique problème : ce sera déjà très bien. Par contre, il faut justifier sa solution et être rigoureux.
Pour répondre, c'est par mail à l'adresse paradoxe_ephemere@yahoo.fr , en n'oubliant pas de préciser votre pseudo.
Les réponses doivent parvenir avant midi du dimanche qui suit le moment où les problèmes ont été posés.
Il n'est pas nécessaire de répondre à chaque problème pour m'envoyer une solution. On peut même me renvoyer la solution d'un seul et unique problème : ce sera déjà très bien. Par contre, il faut justifier sa solution et être rigoureux.
Pour répondre, c'est par mail à l'adresse paradoxe_ephemere@yahoo.fr , en n'oubliant pas de préciser votre pseudo.
Les réponses doivent parvenir avant midi du dimanche qui suit le moment où les problèmes ont été posés.
Dernière édition par le Dim 24 Sep 2006 - 9:06, édité 1 fois

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Problèmes posés le dimanche 24 septembre 2006.
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 1 octobre 2006 à midi.
Problème 1.
Soit ABC un triangle rectangle en A. Si |AB|=15 et |AC|=20, calculer la longueur de la hauteur du triangle ABC issue de A.
Problème 2.
Combien existe-t-il de multiples de 3 qui s'écrirent (en base 10) avec exactement 3 chiffres dont un au moins est un 3 ?
Problème 3.
Dans un plan muni d'un repère orthonormé, existe-t-il un triangle équilatéral dont les trois sommets ont tous une abscisse de valeur entière et une ordonnée de valeur entière ?
Problème 4.
On se place dans l'ensemble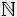 des nombres naturels.
des nombres naturels.
a) Trouver le plus petit nombre qui a exactement 7 diviseurs.
b) Trouver le plus petit nombre qui a exactement 999 diviseurs.
Problème 5.
Une personne saine d'esprit est une personne qui ne se trompe pas dans ce qu'elle croit et une personne folle est une personne qui se trompe systématiquement dans ce qu'elle croit. On considère un asile dans lequel chaque personne est soit saine d'esprit, soit folle. Dans cet asile, chaque personne est également soit un médecin, soit un patient. Il y a au moins une personne saine d'esprit dans cet asile. Une personne est dite particulière si elle croit être un patient. Une personne est dite spéciale si tous les patients croient qu'elle est particulière et que tous les médecins croient qu'elle n'est pas particulière. Dans cet asile, chaque personne a une personne préférée. À chaque fois qu'une personne X croit qu'une personne Y est spéciale, la personne préférée de X croit que Y est un patient. Les personnes A et B sont deux médecins distincts de cet asile. Le médecin A croit que tous les médecins sont sains d'esprit et croit aussi que au moins un patient est fou. Le médecin B croit que tous les patients sont fous et croit aussi qu'au moins un des médecins est sain d'esprit. Le médecin B croit également que le médecin A est sain d'esprit. Prouver que tous les médecins de l'asile sont fous et que tous les patients de l'asile sont sain d'esprit.
Bon amusement !
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 1 octobre 2006 à midi.
Problème 1.
Soit ABC un triangle rectangle en A. Si |AB|=15 et |AC|=20, calculer la longueur de la hauteur du triangle ABC issue de A.
Problème 2.
Combien existe-t-il de multiples de 3 qui s'écrirent (en base 10) avec exactement 3 chiffres dont un au moins est un 3 ?
Problème 3.
Dans un plan muni d'un repère orthonormé, existe-t-il un triangle équilatéral dont les trois sommets ont tous une abscisse de valeur entière et une ordonnée de valeur entière ?
Problème 4.
On se place dans l'ensemble
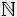 des nombres naturels.
des nombres naturels.a) Trouver le plus petit nombre qui a exactement 7 diviseurs.
b) Trouver le plus petit nombre qui a exactement 999 diviseurs.
Problème 5.
Une personne saine d'esprit est une personne qui ne se trompe pas dans ce qu'elle croit et une personne folle est une personne qui se trompe systématiquement dans ce qu'elle croit. On considère un asile dans lequel chaque personne est soit saine d'esprit, soit folle. Dans cet asile, chaque personne est également soit un médecin, soit un patient. Il y a au moins une personne saine d'esprit dans cet asile. Une personne est dite particulière si elle croit être un patient. Une personne est dite spéciale si tous les patients croient qu'elle est particulière et que tous les médecins croient qu'elle n'est pas particulière. Dans cet asile, chaque personne a une personne préférée. À chaque fois qu'une personne X croit qu'une personne Y est spéciale, la personne préférée de X croit que Y est un patient. Les personnes A et B sont deux médecins distincts de cet asile. Le médecin A croit que tous les médecins sont sains d'esprit et croit aussi que au moins un patient est fou. Le médecin B croit que tous les patients sont fous et croit aussi qu'au moins un des médecins est sain d'esprit. Le médecin B croit également que le médecin A est sain d'esprit. Prouver que tous les médecins de l'asile sont fous et que tous les patients de l'asile sont sain d'esprit.
Bon amusement !
Dernière édition par le Sam 7 Oct 2006 - 13:53, édité 1 fois

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
solutions 1 à 4 postées ! 

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Je confirme la réception des solutions 1 à 4 de le-duche.

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
*** Problème 1 ***
Soit H le pied de la hauteur issue de A.
Le triangle AHC est rectangle en H, et a un angle commun avec le triangle ABC qui est lui aussi rectangle. Ces deux triangles sont donc semblable, avec un rapport de longeur de |AC| / |BC| = 20 / 25 = 4/5.
On a les meme proportions entre AB et AH.
Ainsi |AH| = 4/5 * |AB| = 4*15/5 = 12.
Très bien : problème réussi.
*** Problème 2 ***
Un nombre est multiple de 3 si la somme de ses chiffre est un multiple de 3.
On a un nombre à trois chiffres abc.
Fixons a = 3.
Il faut alors que bc soit un multiple de 3. Il s'agit donc de compter les multiples de 3 entre 10 et 99.
Entre 1 et 99 il y a 99/3 = 33 multiples de 3, auxquels il faut enlever 3, 6 et 9. On a donc 30 multiples de 3 à deux chiffres.
De même en fixant b = 3 et c = 3 on a chaque fois 30 multiples de 3 disponibles.
cela nous fait un total de 90 multiples de 3.
cependant, on a compté plusieurs fois les multiple de 3 contenant plusieurs fois le chiffre 3.
Par le principe d'inclusion - exclusion, on va décompter les multiple contenant au mons deux chiffres 3. dans ce cas on aura alors supprimé le comptage des nombre contenant 3 fois le chiffre 3 (c'est à dire l'unique 333), qu'il faudra ajouter au total obtenu.
Fixons a = b = 3. On a alors c qui peut prendre les valeurs 0 , 3 , 6 , 9 , ce qui nous offre 4 multiples à chaque fois.
En faisant de meme pour a = c = 3 et b = c = 3, on obtient qu'il faut soustraire 12 au total obtenu, soit 90 - 12 = 78.
On a vu qu'à ce stade 333 n'avait pas été compté, on a donc 79 multiple de 3 à 3 chiffres contenant le chiffre 3 au moins une fois.
MAIS ! Dans notre raisonnement, on a admis que les deux premiers chiffres pouvaient éventuellement être 0.
Il faudrait donc maintenant soustraire les nombre à 2 chiffres et à un chiffre étant multiple de 3 et contenant un 3.
On fixe le premier chiffre à 3, et on a alors 4 possibilités (30 33 36 39), puis on fixe le second chiffre à 3, et on a 4 possibilité (3 33 63 93). De nouveau, on a compter 33 deux fois, ce qui nous fait un total de 7 nombres.
On soustrait 7 de 79, ce qui nous donne notre réponse définitive = 72.
Non, il y en a plus que cela. La solution est pas mal quand même, mais le probème n'est pas réussi.
*** Problème 3 ***
Sans perte de généralité, on peut placer notre premier point A du triangle ABC à l'origine (0,0).
Nos deux autres points se trouvent sur un cercle de rayon R variable et séparé par un angle de 60°.
Plaçons nous dans le plan complexe. Notre point B est donc le complexe b1 + i b2 et notre point C le complexe c1 + i c2.
Etant donné l'angle qui les sépare, onfiltered= B*(1/2 + i V3/2), c'est à dire
(c1 + i c2) = (b1 + i b2)(1/2 + i V3/2) = (b1/2 - b2*V3/2) + i (b2/2 + b1*V3/2)
Ainsi, si b1 et b2 sont entiers, alors c1 est entier si et seulement si b2 = 0, et c2 est entier si et seulement si b1 = 0.
On ne peut donc pas avoir b1,b2,c1 et c2 entiers.
Il n'est donc pas possible de construire un tel triangle.
Très bien : problème réussi. Attention cependant à l'emplois un peu abusif des si et seulement si.
*** Problème 4 ***
Partie 1:
Soit un naturel et sa décomposition en facteurs premiers N = p1^a1 * p2^a2 * p3^a3 * ... * pk^ak
Le nombre D de diviseurs de N est D = (a1+1)(a2+1)(a3+1)...(ak+1)
Si D = 7, alors seul l'un des aj est non nul et vaut 6.
Ainsi N vaut alors pj^6.
Pour que N soit le plus petit possible, il faut que j = 1, c'est à dire que pj = 2.
onfiltered= 2^6 = 64.
Partie 2:
onfiltered= p1^a1 * p2^a2 * p3^a3 * ... * pk^ak
Et D le nombre de diviseurs de N.
onfiltered= 999 = 3*3*3*37
Pour avoir un N minimum, une condition necessaire est déjà que l'on se ramène à
D = 999 = 3*3*3*37 = (a1+1)(a2+1)(a3+1)(a4+1)
avec eventuellement certains aj = 0.
On impose aussi que a1 >= a2 >= a3 >= a4.
Les différentes possibilités de décompositions de 999 sont:
999 * 1 * 1 * 1
333 * 3 * 1 * 1
111 * 9 * 1 * 1
37 * 27 * 1 * 1
111 * 3 * 3 * 1
37 * 9 * 3 * 1
37 * 3 * 3 * 3
fournissant des valeurs pour N de respectivement
2^998 = 2,678771518e+300
2^332 * 3^2 = 7,874102609e+100
2^110 * 3^8 = 8,516664922e+36
2^36 * 3^26 = 1,746756897e+23
2^110 * 3^2 * 5^2 = 2,920666983e+35
2^36 * 3^8 * 5^2 = 1,127171217e+16
2^36 * 3^2 * 5^2 * 7^2 = 7,57632231e+14
On voit que le plus petit N est fournit par la dernière possibilité et vaut plus exactement 757632231014400
Très bien : problème réussi.
Cela fait 3 problèmes bien résolu pour le_duche. Trois points de plus que tous les autres.

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
J'ai trouvé mon erreur dans le problème 2.
Quand j'affirme qu'après avoir fixé le premier chiffre à 3, il me faut compter les multiples de 3 à deux chiffres, j'ote les multiples de 3 à un chiffre (3,6 et 9) de mon comptage, ce qui me fait exclure 303,306,309. D'autre part, je ne prend pas en compte le nombre 300...
Je reprend donc mon raisonnement:
Un nombre naturel est un multiple de 3 si et seulement si la somme de ses chiffres est un multiple de 3.
Fixons notre premier chiffre à 3.
Alors nous devons compter tous les nombre à 2 chiffres ou à 1 chiffre qui sont multiples de 3. Il y en a 99/3 pour aller de 99 à 3, auxquels on ajoute le 0, ce qui nous fournit au total 34 multiples de 3 commençant par un 3.
Notons que parmis eux, il y a les nombres 303,330,333,336,339,363,393; tous les autres ne comportant qu'un seul chiffre 3.
Fixons notre deuxième chiffre à 3.
Alors nous devons compter tous les nombres à 2 chiffres qui sont multiples de 3 (et cette fois ils doivent avoir deux chiffres, dont le premier non nul).
Il y en a 99/3 pour aller de 99 à 3, mais il faut oter 3, 6 et 9. On obtient donc 30 nombres multiples de 3 dont le deuxième chiffre est 3.
Notons que parmis eux, il y a les nombres 330,333,336,339,633,933; tous les autres ne comportant qu'un seul chiffre 3.
De la même manière, en fixant notre troisième chiffre à 3, nous trouvons 30 nombres multiples de 3 dont le troisième chiffre est 3.
Notons que parmis eux, il y a les nombres 303,333,363,393,633,933; tous les autres ne comportant qu'un seul chiffre 3.
Certains nombres ont été comptés plusieurs fois. Le nombres ne comportant qu'un seul chiffre 3, n'ont pas pas peu être compté plus d'une fois. Mais les nombres 303,330,336,339,363,393,633,933 ont été comptés deux fois, et le nombre 333 a été compté trois fois.
Notre total est donc 34+30+30-8-2 = 84
(désolé pour cette double faute dans mon raisonnement...)
Quand j'affirme qu'après avoir fixé le premier chiffre à 3, il me faut compter les multiples de 3 à deux chiffres, j'ote les multiples de 3 à un chiffre (3,6 et 9) de mon comptage, ce qui me fait exclure 303,306,309. D'autre part, je ne prend pas en compte le nombre 300...
Je reprend donc mon raisonnement:
Un nombre naturel est un multiple de 3 si et seulement si la somme de ses chiffres est un multiple de 3.
Fixons notre premier chiffre à 3.
Alors nous devons compter tous les nombre à 2 chiffres ou à 1 chiffre qui sont multiples de 3. Il y en a 99/3 pour aller de 99 à 3, auxquels on ajoute le 0, ce qui nous fournit au total 34 multiples de 3 commençant par un 3.
Notons que parmis eux, il y a les nombres 303,330,333,336,339,363,393; tous les autres ne comportant qu'un seul chiffre 3.
Fixons notre deuxième chiffre à 3.
Alors nous devons compter tous les nombres à 2 chiffres qui sont multiples de 3 (et cette fois ils doivent avoir deux chiffres, dont le premier non nul).
Il y en a 99/3 pour aller de 99 à 3, mais il faut oter 3, 6 et 9. On obtient donc 30 nombres multiples de 3 dont le deuxième chiffre est 3.
Notons que parmis eux, il y a les nombres 330,333,336,339,633,933; tous les autres ne comportant qu'un seul chiffre 3.
De la même manière, en fixant notre troisième chiffre à 3, nous trouvons 30 nombres multiples de 3 dont le troisième chiffre est 3.
Notons que parmis eux, il y a les nombres 303,333,363,393,633,933; tous les autres ne comportant qu'un seul chiffre 3.
Certains nombres ont été comptés plusieurs fois. Le nombres ne comportant qu'un seul chiffre 3, n'ont pas pas peu être compté plus d'une fois. Mais les nombres 303,330,336,339,363,393,633,933 ont été comptés deux fois, et le nombre 333 a été compté trois fois.
Notre total est donc 34+30+30-8-2 = 84
(désolé pour cette double faute dans mon raisonnement...)

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Là, c'est la bonne réponse. 

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Problèmes posés le samedi 7 octobre 2006.
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 15 octobre 2006 à midi.
Problème 1.
On considère un polynôme p(x) à coefficents réels. Si le reste de la division euclidienne de ce polynôme par x²-1 est x+5, que vaut le reste de la division euclidienne de ce polynôme par x+1 ?
Problème 2.
Quand tu auras l'âge que j'ai, j'aurai quatre fois l'âge que tu avais lorsque j'avais l'âge que tu as. Un an après ce moment-là, nous aurons exactement un siècle à nous deux. Quel est mon âge actuel ?
Problème 3.
On considère trois cercles deux à deux sécants. Montrer que les trois droites sécantes déterminées en considérant les cercles sécants deux à deux sont concourantes.
Problème 4.
On considère un nombre entier strictement positif n. On écrit n en base 10 et on constate qu'il possède exactement 4 chiffres dont la somme est un multiple de 9. On écrit n en base 9 et on constate qu'il possède exactement 5 chiffres dont la somme est un multiple de 8. Pour toute valeur entière de b allant de 2 à 8 (inclus), on constate que la somme des chiffres de n lorsqu'il est écrit en base b est un multiple de b-1. Déterminer le nombre n.
Problème 5.
Le même problème numéro 5 que la fois dernière, puisque j'avais fait une erreur dans l'énoncé. Je l'ai corrigée en rouge. Désolé.
Bon amusement !
Classement actuel
1. le_duche : 3 points sur 4 possible
2. les autres : 0 point sur 4 possible
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 15 octobre 2006 à midi.
Problème 1.
On considère un polynôme p(x) à coefficents réels. Si le reste de la division euclidienne de ce polynôme par x²-1 est x+5, que vaut le reste de la division euclidienne de ce polynôme par x+1 ?
Problème 2.
Quand tu auras l'âge que j'ai, j'aurai quatre fois l'âge que tu avais lorsque j'avais l'âge que tu as. Un an après ce moment-là, nous aurons exactement un siècle à nous deux. Quel est mon âge actuel ?
Problème 3.
On considère trois cercles deux à deux sécants. Montrer que les trois droites sécantes déterminées en considérant les cercles sécants deux à deux sont concourantes.
Problème 4.
On considère un nombre entier strictement positif n. On écrit n en base 10 et on constate qu'il possède exactement 4 chiffres dont la somme est un multiple de 9. On écrit n en base 9 et on constate qu'il possède exactement 5 chiffres dont la somme est un multiple de 8. Pour toute valeur entière de b allant de 2 à 8 (inclus), on constate que la somme des chiffres de n lorsqu'il est écrit en base b est un multiple de b-1. Déterminer le nombre n.
Problème 5.
Le même problème numéro 5 que la fois dernière, puisque j'avais fait une erreur dans l'énoncé. Je l'ai corrigée en rouge. Désolé.
Bon amusement !
Classement actuel
1. le_duche : 3 points sur 4 possible
2. les autres : 0 point sur 4 possible

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Le problème n°4 est flou, je le réécrit, dis moi si c'est bien ca !
On considère un nombre entier strictement positif n. On écrit n en base 10 et on constate qu'il possède exactement 4 chiffres et que leur somme est un multiple de 9. On écrit n en base 9 et on constate qu'il possède exactement 5 chiffres et que leur somme est un multiple de 8. Pour toute valeur entière de b allant de 2 à 8 (inclus), on constate que la somme des chiffres de n lorsqu'il est écrit en base b est un multiple de b-1. Déterminer le nombre n.
On considère un nombre entier strictement positif n. On écrit n en base 10 et on constate qu'il possède exactement 4 chiffres et que leur somme est un multiple de 9. On écrit n en base 9 et on constate qu'il possède exactement 5 chiffres et que leur somme est un multiple de 8. Pour toute valeur entière de b allant de 2 à 8 (inclus), on constate que la somme des chiffres de n lorsqu'il est écrit en base b est un multiple de b-1. Déterminer le nombre n.

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
solutions 1 à 3 postées

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
le_duche a écrit:On considère un nombre entier strictement positif n. On écrit n en base 10 et on constate qu'il possède exactement 4 chiffres et que leur somme est un multiple de 9. On écrit n en base 9 et on constate qu'il possède exactement 5 chiffres et que leur somme est un multiple de 8. Pour toute valeur entière de b allant de 2 à 8 (inclus), on constate que la somme des chiffres de n lorsqu'il est écrit en base b est un multiple de b-1. Déterminer le nombre n.
Oui, c'est bien ça.

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
le_duche a écrit:solutions 1 à 3 postées
Reçues. Voici les solutions envoyées.
Très bien. Problème 1 réussi.le_duche a écrit:Problème n°1:
Le reste de la division de P(x) par x²-1 est x+5.
Cela signifie qu'il existe un polynome à coefficients réels Q(x) tel que P(x) = (x²-1) Q(x) + (x+5)
Ou encore que P(x) = (x+1)(x-1)Q(x) + (x+5)
En posant lo polynome R(x) = (x-1)Q(x) + 1, on obtient que
P(x) = (x+1)R(x) + 4 =
ce qui signifie en d'autre termes que le reste de la division euclidienne de P(x) par (x+1) vaut 4.
Très bien. Problème 2 réussi.le_duche a écrit:Problème n°2:
Soit x l'age de la personne qui parle, et soit y l'age de la personne à laquelle elle s'adresse, et ce à l'instant de la phrase.
"Quand tu auras l'âge que j'ai" implique que x >= y, et signifie "dans (x-y) an(s)".
"l'âge que tu avais lorsque j'avais l'âge que tu as" vaut y-(x-y) = 2y-x, et implique que 2y >= x.
"quatre fois l'âge que tu avais lorsque j'avais l'âge que tu as" vaut 8y-4x.
"Quand tu auras l'âge que j'ai, j'aurai quatre fois l'âge que tu avais lorsque j'avais l'âge que tu as" se traduit par "Dans (x-y) ans, mon age sera (8y-4x)" ce qui implique l'égalité x+(x-y) = 8y-4x, ou encore 6x = 9y, qui se simplifie en 2x = 3y.
"Un an après ce moment-là" = "quand j'aurai (2x-y+1), et que tu auras (x+1)"
"nous aurons exactement un siècle à nous deux" signifie que (2x-y+1) + (x+1) = 100 qui se simplifie en 3x-y = 98.
On a donc le systeme d'équations:
{ 2x = 3y
{ 3x-y = 98
qui a pour unique solution
{ x = 42
{ y = 28
La réponse à la question est donc x = 42.
Non car les rayons des cercles ne sont pas nécessairement égaux. Problème 3 non résolu.le_duche a écrit:Problème n°3:
Les centre des trois cercles forment un triangle ABC.
Les droites déterminées en considérant les cercles sécants deux à deux sont les médiatrices de ce triangle.
Les médiatrices d'un triangles sont concourantes (et leur intersection est le centre du cercle circonscrit au triangle).
Dernière édition par le Dim 15 Oct 2006 - 10:41, édité 3 fois

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Problèmes posés le dimanche 15 octobre 2006.
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 22 octobre 2006 à midi.
Problème 1.
Un ange ne dit jamais le contraire de ce qu'il pense. Un démon ne dit jamais ce qu'il pense. Un humain dit parfois ce qu'il pense et parfois le contraire de ce qu'il pense. On sait que Nöy, Elfomiss et Sarah sont un ange, une humaine et un démon, mais on ne sait pas qui est quoi. Par contre, elles, elles le savent très bien et voici ce qu'elles en disent.
Sarah : - C'est Nöy le démon.
Nöy : - C'est Sarah le démon.
Elphomiss : - Je suis le démon.
Nöy : - C'est Elphomiss le démon.
Qui est l'humaine, qui est l'ange, qui est le démon ?
Problème 2.
On considère un triangle acutangle ABC. Soit D la projection orthogonale de A sur [BC]. Soit X un point de [BC] différent de B et C. Soit E la projection orthogonale de B sur [CA]. Soit Y un point de [CA] différent de C et A. Soit F la projection orthogonale de C sur [AB]. Soit Z un point de [AB] différent de A et B. Prouver que le périmètre du triangle DEF est inférieur ou égal au périmètre du triangle XYZ et qu'on a l'égalité si et seulement si X=D, Y=E et Z=F.
Problème 3.
a) Trouver toutes les surjections f de dans
dans  qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.
qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.
b) Trouver toutes les injections f de dans
dans  qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.
qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.
Problème 4.
Deux joueurs jouent au jeu suivant. On dispose d'un plan pavé par des hexagones réguliers isométriques. Chacun à leur tour, les joueurs vont s'approprier un hexagone qui n'a pas encore été approprié. Le but pour le premier joueur est de s'approprier N hexagones consécutifs et alignés (selon une des trois directions principales que les hexagones délimitent).
Existe-t-il un entier strictement positif N pour lequel le second joueur peut empêcher le premier joueur d'arriver à son but quelle que soit la façon dont le premier joueur joue ? Si oui, trouver la plus petite valeur possible d'un tel entier N.
Bon amusement !
Classement actuel
1. le_duche : 5 points sur 9 possible
2. les autres : 0 point sur 9 possible
NB : j'accepte encore les premières solutions correctes de chacuns des problèmes 3, 4, 5 de la semaine passé.
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 22 octobre 2006 à midi.
Problème 1.
Un ange ne dit jamais le contraire de ce qu'il pense. Un démon ne dit jamais ce qu'il pense. Un humain dit parfois ce qu'il pense et parfois le contraire de ce qu'il pense. On sait que Nöy, Elfomiss et Sarah sont un ange, une humaine et un démon, mais on ne sait pas qui est quoi. Par contre, elles, elles le savent très bien et voici ce qu'elles en disent.
Sarah : - C'est Nöy le démon.
Nöy : - C'est Sarah le démon.
Elphomiss : - Je suis le démon.
Nöy : - C'est Elphomiss le démon.
Qui est l'humaine, qui est l'ange, qui est le démon ?
Problème 2.
On considère un triangle acutangle ABC. Soit D la projection orthogonale de A sur [BC]. Soit X un point de [BC] différent de B et C. Soit E la projection orthogonale de B sur [CA]. Soit Y un point de [CA] différent de C et A. Soit F la projection orthogonale de C sur [AB]. Soit Z un point de [AB] différent de A et B. Prouver que le périmètre du triangle DEF est inférieur ou égal au périmètre du triangle XYZ et qu'on a l'égalité si et seulement si X=D, Y=E et Z=F.
Problème 3.
a) Trouver toutes les surjections f de
 dans
dans  qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.
qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.b) Trouver toutes les injections f de
 dans
dans  qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.
qui vérifie l'égalité f(f(x))=-f(x) quel que soit le nombre entier x.Problème 4.
Deux joueurs jouent au jeu suivant. On dispose d'un plan pavé par des hexagones réguliers isométriques. Chacun à leur tour, les joueurs vont s'approprier un hexagone qui n'a pas encore été approprié. Le but pour le premier joueur est de s'approprier N hexagones consécutifs et alignés (selon une des trois directions principales que les hexagones délimitent).
Existe-t-il un entier strictement positif N pour lequel le second joueur peut empêcher le premier joueur d'arriver à son but quelle que soit la façon dont le premier joueur joue ? Si oui, trouver la plus petite valeur possible d'un tel entier N.
Bon amusement !
Classement actuel
1. le_duche : 5 points sur 9 possible
2. les autres : 0 point sur 9 possible
NB : j'accepte encore les premières solutions correctes de chacuns des problèmes 3, 4, 5 de la semaine passé.

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
pfff j'oublie toujours une connerie dans ce genre...
c'est vrai que c'était beaucoup plus facile du coup ^^
c'est vrai que c'était beaucoup plus facile du coup ^^

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Pour le 3 la questions est pas super claire, car préciser que l'on a la propriété pour tout x entier, c'est une façon de dire que c'est une injection...
Donc ca transformerait le problème en cherchant l'ensemble des bijections pour le a) et l'ensemble des surjections pour le b)
faut m'éclairer un peu là !
Donc ca transformerait le problème en cherchant l'ensemble des bijections pour le a) et l'ensemble des surjections pour le b)
faut m'éclairer un peu là !

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Problème 3.
a) Trouver toutes les surjections f de dans
dans  qui vérifie la propriété
qui vérifie la propriété 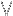 x
x 
 , f(f(x))=-f(x).
, f(f(x))=-f(x).
b) Trouver toutes les injections f de dans
dans  qui vérifie la propriété
qui vérifie la propriété 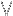 x
x 
 , f(f(x))=-f(x).
, f(f(x))=-f(x).
Si tu ne comprends toujours pas mon langage redemande encore. Cela me semble clair, mais les conventions des uns ne sont pas toujours celle des autres.
a) Trouver toutes les surjections f de
 dans
dans  qui vérifie la propriété
qui vérifie la propriété 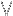 x
x 
 , f(f(x))=-f(x).
, f(f(x))=-f(x).b) Trouver toutes les injections f de
 dans
dans  qui vérifie la propriété
qui vérifie la propriété 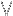 x
x 
 , f(f(x))=-f(x).
, f(f(x))=-f(x).Si tu ne comprends toujours pas mon langage redemande encore. Cela me semble clair, mais les conventions des uns ne sont pas toujours celle des autres.

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Ben disons que je pars du principe que si on affirme
pour tout a appartenant à broll, alors f(a)=...
j'en conclu que f(a) est défini pour tout a...
Dans le cas d'une surjection, si elle est définie pour tout point de son ensemble d'origine, alors c'est une bijection... non ?
pour tout a appartenant à broll, alors f(a)=...
j'en conclu que f(a) est défini pour tout a...
Dans le cas d'une surjection, si elle est définie pour tout point de son ensemble d'origine, alors c'est une bijection... non ?

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
le_duche a écrit:Dans le cas d'une surjection, si elle est définie pour tout point de son ensemble d'origine, alors c'est une bijection... non ?
Non. Il faut l'injection aussi.
DEFINITION
Soient A et B deux ensembles.
Une application f de A dans B est une loie qui à tout élément de A associe un élément de B. On note f(x) l'élément associé à x.
Une application de A dans B est injective (ou une injection) si
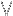 x,y
x,y  A, on a l'implication f(x)=f(y)
A, on a l'implication f(x)=f(y)  x=y.
x=y.Une application de A dans B est surjective (ou une surjection) si
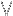 y
y  B
B 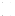 x
x  A tel que f(x)=y.
A tel que f(x)=y.Une application de A dans B est bijective (ou une bijection) si elle est à la fois injective et surjective.

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Wep ok, j'avais mal cerné la définition d'injection... 

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
[quote="ephemere"]Problèmes posés le samedi 21 octobre 2006.
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 5 novembre 2006 à midi.
Problème 1.
On considère un cercle de rayon 1. Sur ce cercle, on considère trois points A, B et C qui sont tels que l'angle <ABC mesure 60°. On demande de calculer la longueur de la corde [AC].
Problème 2.
Une tour cylindrique parfaitement verticale possède neuf étages identiques. Si on se place au niveau du pied de la tour à exactement cent mètres de celle-ci, on peut voir exactement les huit étages du bas sous un certain angle A. Du même endrois, on peut voir exactement les trois étages du bas sous l'angle A/2. Trouver la hauteur de la tour.
Problème 3.
Si x est un entier strictement positif, on note x! le produit de tous les entiers strictement positifs et au plus égaux à x.
Prouver que pour tout couple d'entiers strictement positifs (a,b),
le nombre ((ab)!)² est divisible par le nombre (a!)^{b+1}(b!)^{a+1}.
Problème 4.
On veut colorier les sommets d'un polygone régulier de 100 côtés avec 50 couleurs différentes en utilisant exactement deux fois chaque couleur. Prouver qu'il existe nécessairement deux couleurs A et B telles que la distance qui sépare les deux sommets de couleur A soit égale à la distance qui sépare les deux sommets de couleur B.
Bon amusement !
Les solutions doivent parvenir par mail à l'adresse paradoxe_ephemere@yahoo.fr avant le 5 novembre 2006 à midi.
Problème 1.
On considère un cercle de rayon 1. Sur ce cercle, on considère trois points A, B et C qui sont tels que l'angle <ABC mesure 60°. On demande de calculer la longueur de la corde [AC].
Problème 2.
Une tour cylindrique parfaitement verticale possède neuf étages identiques. Si on se place au niveau du pied de la tour à exactement cent mètres de celle-ci, on peut voir exactement les huit étages du bas sous un certain angle A. Du même endrois, on peut voir exactement les trois étages du bas sous l'angle A/2. Trouver la hauteur de la tour.
Problème 3.
Si x est un entier strictement positif, on note x! le produit de tous les entiers strictement positifs et au plus égaux à x.
Prouver que pour tout couple d'entiers strictement positifs (a,b),
le nombre ((ab)!)² est divisible par le nombre (a!)^{b+1}(b!)^{a+1}.
Problème 4.
On veut colorier les sommets d'un polygone régulier de 100 côtés avec 50 couleurs différentes en utilisant exactement deux fois chaque couleur. Prouver qu'il existe nécessairement deux couleurs A et B telles que la distance qui sépare les deux sommets de couleur A soit égale à la distance qui sépare les deux sommets de couleur B.
Bon amusement !
Dernière édition par le Sam 21 Oct 2006 - 21:53, édité 1 fois

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
Je vais avoir un peu moins de temps pour chercher sur tes problèmes ces temps ci... tu devrais peut etre les laisser deux semaines plutot qu'une ! 

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Les problèmes d'Ephemere
Re: Les problèmes d'Ephemere
D'accord. J'édite la date de remise.

ephemere- Membre

-
 Nombre de messages : 633
Nombre de messages : 633
Age : 45
Localisation : Belgique
Profession / Etudes : Étudiant de 3ème cycle
Points : 7146
Date d'inscription : 05/05/2005
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
» Devoir maison sur équilibre et réaction chimique
» Ma présentation
» projet scientique sur la LUMIERE
» La trajectoire de la Terre
» Equilibrer une réaction redox
» les effets sur les lignes de transport de l’électricité
» lignes de transport de l'électricité
» Gravitation
» Maquette suspension de moto 2D