Problème n°5
3 participants
Page 1 sur 1
 Problème n°5
Problème n°5
Démontrer qu'il existe une infinité de naturels a tels que n4+a ne soit jamais premier pour aucune valeur de n.

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Problème n°5
Re: Problème n°5
La condition sur n est n >= 0 ou n > 0 ?

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Problème n°5
Re: Problème n°5
On va dire n>0...

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Problème n°5
Re: Problème n°5
Il est coriace !
Je rechercherai dans quelques jours, là je vois pas.
Je rechercherai dans quelques jours, là je vois pas.

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Problème n°5
Re: Problème n°5
Je n'ai rien démontré du tout, mais j'ai une conjecture.
On remarque que le chiffre des unités des puissances quatrièmes d'entiers naturels peut prendre seulement ces valeurs: 1 6 5 0.
Ainsi, on pourrait essayer d'ajouter "a", tel que n^4+a ne soit jamais un nombre premier on considérant cette observation.
Donc je me suis dit que je pourrais essayer de prouver que que si a=10x+4 avec x
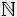 *, n^4+a est toujours un multiple d'un autre nombre...
*, n^4+a est toujours un multiple d'un autre nombre...
Et on aurait alors une infinité de naturels a tels que n^4+a ne soit jamais premier pour aucune valeur de n.
Mais je n'ai pas du tout commencé à démontrer ça.
C'était juste une piste... Serait-il possible de me dire si je ne m'égare pas du problème avant que je me lance dans une recherche qui n'aboutira peut être jamais ?
On remarque que le chiffre des unités des puissances quatrièmes d'entiers naturels peut prendre seulement ces valeurs: 1 6 5 0.
Ainsi, on pourrait essayer d'ajouter "a", tel que n^4+a ne soit jamais un nombre premier on considérant cette observation.
Donc je me suis dit que je pourrais essayer de prouver que que si a=10x+4 avec x

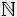 *, n^4+a est toujours un multiple d'un autre nombre...
*, n^4+a est toujours un multiple d'un autre nombre...Et on aurait alors une infinité de naturels a tels que n^4+a ne soit jamais premier pour aucune valeur de n.
Mais je n'ai pas du tout commencé à démontrer ça.
C'était juste une piste... Serait-il possible de me dire si je ne m'égare pas du problème avant que je me lance dans une recherche qui n'aboutira peut être jamais ?

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Problème n°5
Re: Problème n°5
(précision pour la conjecture: si n>0 alors le a=10x+4 avec x appartenant à tous les naturels)

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Problème n°5
Re: Problème n°5
Bon, il se fait tard alors je vais te donner un indice. Il y a du vrai dans ce que t'as écrit mais je n'ai pas le temps de m'y pencher dessus ce soir !
Indice : soit a=4b4...
Indice : soit a=4b4...

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Problème n°5
Re: Problème n°5
Cette conjecture est fausse.
Ce que tu as remarqué c'est ceci, mais sans vraiment le voir.
Si on regarde les valeurs de n^4 modulo 2,3, et 5 on a
0^4 = 0 (mod 2)
1^4 = 1 (mod 2)
0^4 = 0 (mod 3)
1^4 = 1 (mod 3)
2^4 = 16 = 1 (mod 3)
0^4 = 0 (mod 5)
1^4 = 1 (mod 5)
2^4 = 16 = 1 (mod 5)
3^4 = 81 = 1 (mod 5)
4^4 = 256 = 1 (mod 5)
Cela signifie que si l'on choisi un a = -1 (mod 5) par exemple, n^4+a sera toujours divisible par 5 sauf si n est divisible par 5.
Ca raduit donc le nombre de n "dangereux" (ceux qui créent des premiers).
On peut également combiner, par exemple prendre un a = -1 (mod 2*3*5), ce qui signifie que n^4+a sera toujorus divisible soit par 2 soit par 3 soit par 5, sauf lorsque n est un multiple de 30.
Mais cela ne m'a pas encore mené à quelque chose, il me semble que cette idée tourne en rond. En effet, si on se contente de regarder uniquement les a de la forme a=5b-1 on ne fait que reporter le problème, car il deviendra
Montrer qu'il existe une infinité de b, tels que pour tout m
625 m^4 + 5b - 1 est non premier. Ce qui ne simplfie pas les choses à mon sens ^^
Ce que tu as remarqué c'est ceci, mais sans vraiment le voir.
Si on regarde les valeurs de n^4 modulo 2,3, et 5 on a
0^4 = 0 (mod 2)
1^4 = 1 (mod 2)
0^4 = 0 (mod 3)
1^4 = 1 (mod 3)
2^4 = 16 = 1 (mod 3)
0^4 = 0 (mod 5)
1^4 = 1 (mod 5)
2^4 = 16 = 1 (mod 5)
3^4 = 81 = 1 (mod 5)
4^4 = 256 = 1 (mod 5)
Cela signifie que si l'on choisi un a = -1 (mod 5) par exemple, n^4+a sera toujours divisible par 5 sauf si n est divisible par 5.
Ca raduit donc le nombre de n "dangereux" (ceux qui créent des premiers).
On peut également combiner, par exemple prendre un a = -1 (mod 2*3*5), ce qui signifie que n^4+a sera toujorus divisible soit par 2 soit par 3 soit par 5, sauf lorsque n est un multiple de 30.
Mais cela ne m'a pas encore mené à quelque chose, il me semble que cette idée tourne en rond. En effet, si on se contente de regarder uniquement les a de la forme a=5b-1 on ne fait que reporter le problème, car il deviendra
Montrer qu'il existe une infinité de b, tels que pour tout m
625 m^4 + 5b - 1 est non premier. Ce qui ne simplfie pas les choses à mon sens ^^

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Problème n°5
Re: Problème n°5
Ha ben combiné à ma technique ça marche impec !
Je rédige ça
Je rédige ça

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Problème n°5
Re: Problème n°5
oups non je me suis emballé

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
» Devoir maison sur équilibre et réaction chimique
» Ma présentation
» projet scientique sur la LUMIERE
» La trajectoire de la Terre
» Equilibrer une réaction redox
» les effets sur les lignes de transport de l’électricité
» lignes de transport de l'électricité
» Gravitation
» Maquette suspension de moto 2D