problème avec un DM urgent
2 participants
Page 1 sur 1
 problème avec un DM urgent
problème avec un DM urgent
bonsoir alors voilà j'ai un Dm de maths que jai beaucoup de mal à comprendre et vu que j'ai beaucoup de travail en ce moment j'aurais bien aimer un peu d'aide svp
le but de cet exercice est de démontrer que la fonction f définie sur [0;+infinie[ par f(x]= xsin(x) n'admet pas de limite quand X tend vers + infinie. on désigne par C la courbe de F dans un repère orthonormal du plan.
1) déterminer les absisses des points d'intersection de C et de l'axe des abscisses. on les rangera selon une suite (an)n strcitement croissante. definir chaque terme an en fonction de n.
2) determiner les abscisses des points d'intersection de C et de la droite y=x. on les rangera selon une suite (bn)n strictement croissante. définer chaque terme bn en fonction de n.
3) déterminer les limites éventuelles des suites (an)n; (bn)n; (f(an)n) et (f(bn)n)
4) en déduire que la fonction F ne peut pas admettre de limite en x +inifini
merci d'avance parce que je vois pas comment faire
le but de cet exercice est de démontrer que la fonction f définie sur [0;+infinie[ par f(x]= xsin(x) n'admet pas de limite quand X tend vers + infinie. on désigne par C la courbe de F dans un repère orthonormal du plan.
1) déterminer les absisses des points d'intersection de C et de l'axe des abscisses. on les rangera selon une suite (an)n strcitement croissante. definir chaque terme an en fonction de n.
2) determiner les abscisses des points d'intersection de C et de la droite y=x. on les rangera selon une suite (bn)n strictement croissante. définer chaque terme bn en fonction de n.
3) déterminer les limites éventuelles des suites (an)n; (bn)n; (f(an)n) et (f(bn)n)
4) en déduire que la fonction F ne peut pas admettre de limite en x +inifini
merci d'avance parce que je vois pas comment faire

snoopy70- Membre

-
 Nombre de messages : 79
Nombre de messages : 79
Age : 32
Localisation : 70
Profession / Etudes : terminale S
Points : 6116
Date d'inscription : 30/11/2008
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
Bonsoir,
tu as déjà répondu à quoi ? Quelles sont tes pistes ?
tu as déjà répondu à quoi ? Quelles sont tes pistes ?

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
pour la question 1
je pense qu'il faut que xsinx =0 donc les solutions seront pi 2pi 3pi ....
pis la 2) xsinx=x dc sinx = 1 donc -pi/2 ou pi/2
est ce sa ? et comment bien l'expliquer parce que c'est justes des pistes sa ...
merci d'avance
je pense qu'il faut que xsinx =0 donc les solutions seront pi 2pi 3pi ....
pis la 2) xsinx=x dc sinx = 1 donc -pi/2 ou pi/2
est ce sa ? et comment bien l'expliquer parce que c'est justes des pistes sa ...
merci d'avance

snoopy70- Membre

-
 Nombre de messages : 79
Nombre de messages : 79
Age : 32
Localisation : 70
Profession / Etudes : terminale S
Points : 6116
Date d'inscription : 30/11/2008
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
1) Oui, en commençant par 0. Tu as donc 0,  , 2
, 2  , 3
, 3  , ... Tu en déduis quoi comme suite (an) ?
, ... Tu en déduis quoi comme suite (an) ?
2) C'est le même principe. Mais - /2 ne fait pas partie du domaine de définition de ta fonction f. Du coup, les premiers termes sont 0,
/2 ne fait pas partie du domaine de définition de ta fonction f. Du coup, les premiers termes sont 0,  /2, 3
/2, 3  /2, 5
/2, 5  /2... Je te laisse exprimer la suite (bn).
/2... Je te laisse exprimer la suite (bn).
 , 2
, 2  , 3
, 3  , ... Tu en déduis quoi comme suite (an) ?
, ... Tu en déduis quoi comme suite (an) ?2) C'est le même principe. Mais -
 /2 ne fait pas partie du domaine de définition de ta fonction f. Du coup, les premiers termes sont 0,
/2 ne fait pas partie du domaine de définition de ta fonction f. Du coup, les premiers termes sont 0,  /2, 3
/2, 3  /2, 5
/2, 5  /2... Je te laisse exprimer la suite (bn).
/2... Je te laisse exprimer la suite (bn).
Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
ok merci c'est ce que jai fait et jai trouve
an=npi
et bn= 2n+pi/2
c'est sa ?
apres pour les limites an et bn ont la limite + infini je pense mais comment l'expliquer correctement ?
pour f(an) et f(bn) je pense qu'il faut faire avec un théorème du cours vu que c'est les composé
pis pour la 4 on trouvera pas les meme limites de f(an) et f(bn) donc f n'a pas de limite . en gros c'est sa l'exo non ?
an=npi
et bn= 2n+pi/2
c'est sa ?
apres pour les limites an et bn ont la limite + infini je pense mais comment l'expliquer correctement ?
pour f(an) et f(bn) je pense qu'il faut faire avec un théorème du cours vu que c'est les composé
pis pour la 4 on trouvera pas les meme limites de f(an) et f(bn) donc f n'a pas de limite . en gros c'est sa l'exo non ?

snoopy70- Membre

-
 Nombre de messages : 79
Nombre de messages : 79
Age : 32
Localisation : 70
Profession / Etudes : terminale S
Points : 6116
Date d'inscription : 30/11/2008
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
OK pour an.
Pour bn par contre, c'est pas ça. C'est plutôt (2n+1) /2 ou n+
/2 ou n+  /2.
/2.
Pour les limites, si tu arrives à montrer que les suites sont strictement croissantes et non majorées, alors elles divergent vers +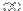 .
.
Pour f(an) et f(bn), soit tu appliques ton théorème du cours, soit tu explicites les termes pour les étudier ensuite.

Pour bn par contre, c'est pas ça. C'est plutôt (2n+1)
 /2 ou n+
/2 ou n+  /2.
/2.Pour les limites, si tu arrives à montrer que les suites sont strictement croissantes et non majorées, alors elles divergent vers +
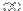 .
.Pour f(an) et f(bn), soit tu appliques ton théorème du cours, soit tu explicites les termes pour les étudier ensuite.
Non c'est faux. Cherche un contre-exemple pour t'en convaincre.pis pour la 4 on trouvera pas les meme limites de f(an) et f(bn) donc f n'a pas de limite

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
comment on peut montrer qu'elles sont non majorées les suites ?
euh j'ai réfléchit à un contre exemple mais je ne vois pas ...
et pourquoi bn jai faut ? désolée avec toutes mes questions idiotes sans doute ^^
euh j'ai réfléchit à un contre exemple mais je ne vois pas ...
et pourquoi bn jai faut ? désolée avec toutes mes questions idiotes sans doute ^^

snoopy70- Membre

-
 Nombre de messages : 79
Nombre de messages : 79
Age : 32
Localisation : 70
Profession / Etudes : terminale S
Points : 6116
Date d'inscription : 30/11/2008
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
Y a pas de questions idiotes. 
"et pourquoi bn jai faut ?"
b0=pi/2, b1=2+pi/2. Ca ne coïncide déjà pas.
"comment on peut montrer qu'elles sont non majorées les suites ?"
Fixe toi un entier N aussi grand que tu veux. Soit uN son terme associé. D'après toi, peux tu trouver un n>N tel que un>uN ?
"euh j'ai réfléchit à un contre exemple mais je ne vois pas ..."
Soit f la fonction qui à x associe x=f(x).
Soit les suites (an) et (bn) telles que an=n et bn=-n.
f(an)=f(n)=n (tend vers +oo)
f(bn)=f(-n)=-n (tend vers -oo).
f(an) et f(bn) n'ont pas la même limite. Et pourtant, f a bien une limite qui est +oo.
"et pourquoi bn jai faut ?"
b0=pi/2, b1=2+pi/2. Ca ne coïncide déjà pas.
"comment on peut montrer qu'elles sont non majorées les suites ?"
Fixe toi un entier N aussi grand que tu veux. Soit uN son terme associé. D'après toi, peux tu trouver un n>N tel que un>uN ?
"euh j'ai réfléchit à un contre exemple mais je ne vois pas ..."
Soit f la fonction qui à x associe x=f(x).
Soit les suites (an) et (bn) telles que an=n et bn=-n.
f(an)=f(n)=n (tend vers +oo)
f(bn)=f(-n)=-n (tend vers -oo).
f(an) et f(bn) n'ont pas la même limite. Et pourtant, f a bien une limite qui est +oo.

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
ok merci
j'ai retravailler le DM cet apres midi
faut que je vois pour la rédaction j'ai du mal pour sa ^^
j'ai retravailler le DM cet apres midi
faut que je vois pour la rédaction j'ai du mal pour sa ^^

snoopy70- Membre

-
 Nombre de messages : 79
Nombre de messages : 79
Age : 32
Localisation : 70
Profession / Etudes : terminale S
Points : 6116
Date d'inscription : 30/11/2008
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
pour la question 4 ) je veux faire un raisonnement par l'absurde. je voudrais savoir si ma rédaction est bonne svp
supposons que f(x)=b avec b un réel donc d'apres le théorème
lim de Un=+infini lim(fx)=b
donc lim (un)=b ( tout sa en + infini bien sur ^^)
donc un ici dans notre cas correspond soit à an ou bn.
donc lim f(an)=f(bn) or il y a une absurdité car lim f(an)=0 et lim f(bn)=+infini
on aurait du avoir limf(an)=limf(bn) pour que lim (un)=b mais ici lim (un) différent de b donc nour pouvons en conclure que la fonction f n'ademt pas de limite
merci de m'aider c'est tres gentil =)
supposons que f(x)=b avec b un réel donc d'apres le théorème
lim de Un=+infini lim(fx)=b
donc lim (un)=b ( tout sa en + infini bien sur ^^)
donc un ici dans notre cas correspond soit à an ou bn.
donc lim f(an)=f(bn) or il y a une absurdité car lim f(an)=0 et lim f(bn)=+infini
on aurait du avoir limf(an)=limf(bn) pour que lim (un)=b mais ici lim (un) différent de b donc nour pouvons en conclure que la fonction f n'ademt pas de limite
merci de m'aider c'est tres gentil =)

snoopy70- Membre

-
 Nombre de messages : 79
Nombre de messages : 79
Age : 32
Localisation : 70
Profession / Etudes : terminale S
Points : 6116
Date d'inscription : 30/11/2008
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
"supposons que f(x)=b avec b un réel donc d'apres le théorème "
f(x) tende vers b quand x tend vers l'infini plutôt
"donc lim (un)=b "
donc lim f(un)=b
Sinon après ça a l'air d'être bon.
f(x) tende vers b quand x tend vers l'infini plutôt
"donc lim (un)=b "
donc lim f(un)=b
Sinon après ça a l'air d'être bon.

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: problème avec un DM urgent
Re: problème avec un DM urgent
ok merci beaucoup =)
voilà fini l'exo =D
voilà fini l'exo =D

snoopy70- Membre

-
 Nombre de messages : 79
Nombre de messages : 79
Age : 32
Localisation : 70
Profession / Etudes : terminale S
Points : 6116
Date d'inscription : 30/11/2008
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
» Devoir maison sur équilibre et réaction chimique
» Ma présentation
» projet scientique sur la LUMIERE
» La trajectoire de la Terre
» Equilibrer une réaction redox
» les effets sur les lignes de transport de l’électricité
» lignes de transport de l'électricité
» Gravitation
» Maquette suspension de moto 2D