Réponse à Butterfly Nebula, concernant la résolution d'un système trigonométrique
Page 1 sur 1
 Réponse à Butterfly Nebula, concernant la résolution d'un système trigonométrique
Réponse à Butterfly Nebula, concernant la résolution d'un système trigonométrique
Réponse à Butterfly Nebula, à propôs de la résolution du système d'équations trigonométriques :
Bonjour Butterfly Nebula
Pour résoudre le système d'équations trigonométriques:
cos a = sin b
sin a = cos b
On se servira des formules:
cos x = sin [( /2) - x] et
/2) - x] et
sin x = cos [( /2) - x]
/2) - x]
Dans le cas qui nous intéresse, nous utiliserons "a" à la place de "x",
et nous n'oublierons pas que quelque soit (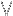 ) un angle "A", il existe (
) un angle "A", il existe ( 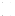 ) un nombre infini d'angles "A + 2k
) un nombre infini d'angles "A + 2k  ",
",
avec k
 , ayant même sinus et même cosinus.
, ayant même sinus et même cosinus.
par exemple:
si A = /6 (soit 30°), cos A =
/6 (soit 30°), cos A =  3/2 et,
3/2 et,
si k = 1, cos (A + 2 ) =
) =  3/2 , A + 2
3/2 , A + 2  = 13
= 13  /6
/6
si k = 2, cos (A+ 4 ) = cos (25
) = cos (25  /6) = (
/6) = ( 3)/2
3)/2
si k = -1, cos (A - 2 ) = cos (-11 :
) = cos (-11 :  /6) = (
/6) = ( 3)/2 .
3)/2 .
Pour en revenir à la résolution de l'exercice, on peut écrire :
cos a = sin[( /2) - a + 2k
/2) - a + 2k  ]
]
sin a = cos [( /2) - a + 2k
/2) - a + 2k  ]
]
k
 .
.
Par comparaison avec les équations de l'énoncé :
cos a = sin b
sin a = cos b
b ]( /2) - a + 2k
/2) - a + 2k  ]
]
a + b = ( /2) + 2k
/2) + 2k 
l'ensemble des solutions est donc :
S = {(a,b)
 ^2 / a + b =
^2 / a + b = 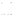 /2 modulo 2k
/2 modulo 2k  , avec k
, avec k 
 }.
}.
On lit :
S égale l'ensemble des couples appartenant à ^2 tels que a plus b égale pi sur deux modulo deux k pi, avec k
^2 tels que a plus b égale pi sur deux modulo deux k pi, avec k
appartenant à
Notes:
 ^2 =
^2 =  croix
croix  ou
ou  au carré
au carré
modulo 2k : à 2k
: à 2k  près.
près.
Vérification:
si a = 2 /3
/3
b = ( /2) - (2
/2) - (2  /3) + 2k
/3) + 2k 
b = -( /6) + 2k
/6) + 2k 
si k = 0:
b = -( /6)
/6)
si k = 1:
b = -( /6) + 2
/6) + 2 
b = 11 /6
/6
si k = 2:
b = -( /6) + 4
/6) + 4 
b = 23 /6
/6
si k = -1 ( k est négatif)
b = -( /6) - 2
/6) - 2 
b = -(13 /6)
/6)
Les angles b [ -( /6) ; 11
/6) ; 11  /6 ; 23
/6 ; 23  /6 ; -(13
/6 ; -(13  :6) ] obtenus sont tous situés au même endroit sur le cercle trigonométrique et ont donc tous même sinus et même cosinus.
:6) ] obtenus sont tous situés au même endroit sur le cercle trigonométrique et ont donc tous même sinus et même cosinus.
Si on fait une vérification :
a = 2 /3, cos a = -(1/2) et sin a = (
/3, cos a = -(1/2) et sin a = (  3)/2
3)/2
si on prend b = -( /6) par exemple : cos b = (
/6) par exemple : cos b = (  3)/2 et sin b = -(1/2)
3)/2 et sin b = -(1/2)
On voit bien que cos a = sin b et sin a = cos b.
Je crois que c'est fini,
j'espère que cela vous aidera
bonne journée.
mi_li_mi
Bonjour Butterfly Nebula
Pour résoudre le système d'équations trigonométriques:
cos a = sin b
sin a = cos b
On se servira des formules:
cos x = sin [(
 /2) - x] et
/2) - x] et sin x = cos [(
 /2) - x]
/2) - x]Dans le cas qui nous intéresse, nous utiliserons "a" à la place de "x",
et nous n'oublierons pas que quelque soit (
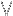 ) un angle "A", il existe (
) un angle "A", il existe ( 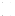 ) un nombre infini d'angles "A + 2k
) un nombre infini d'angles "A + 2k  ",
", avec k

 , ayant même sinus et même cosinus.
, ayant même sinus et même cosinus.par exemple:
si A =
 /6 (soit 30°), cos A =
/6 (soit 30°), cos A =  3/2 et,
3/2 et,si k = 1, cos (A + 2
 ) =
) =  3/2 , A + 2
3/2 , A + 2  = 13
= 13  /6
/6si k = 2, cos (A+ 4
 ) = cos (25
) = cos (25  /6) = (
/6) = ( 3)/2
3)/2si k = -1, cos (A - 2
 ) = cos (-11 :
) = cos (-11 :  /6) = (
/6) = ( 3)/2 .
3)/2 .Pour en revenir à la résolution de l'exercice, on peut écrire :
cos a = sin[(
 /2) - a + 2k
/2) - a + 2k  ]
]sin a = cos [(
 /2) - a + 2k
/2) - a + 2k  ]
]k

 .
.Par comparaison avec les équations de l'énoncé :
cos a = sin b
sin a = cos b
b ](
 /2) - a + 2k
/2) - a + 2k  ]
]a + b = (
 /2) + 2k
/2) + 2k 
l'ensemble des solutions est donc :
S = {(a,b)

 ^2 / a + b =
^2 / a + b = 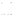 /2 modulo 2k
/2 modulo 2k  , avec k
, avec k 
 }.
}.On lit :
S égale l'ensemble des couples appartenant à
 ^2 tels que a plus b égale pi sur deux modulo deux k pi, avec k
^2 tels que a plus b égale pi sur deux modulo deux k pi, avec k appartenant à

Notes:
 ^2 =
^2 =  croix
croix  ou
ou  au carré
au carrémodulo 2k
 : à 2k
: à 2k  près.
près.Vérification:
si a = 2
 /3
/3b = (
 /2) - (2
/2) - (2  /3) + 2k
/3) + 2k 
b = -(
 /6) + 2k
/6) + 2k 
si k = 0:
b = -(
 /6)
/6)si k = 1:
b = -(
 /6) + 2
/6) + 2 
b = 11
 /6
/6si k = 2:
b = -(
 /6) + 4
/6) + 4 
b = 23
 /6
/6si k = -1 ( k est négatif)
b = -(
 /6) - 2
/6) - 2 
b = -(13
 /6)
/6)Les angles b [ -(
 /6) ; 11
/6) ; 11  /6 ; 23
/6 ; 23  /6 ; -(13
/6 ; -(13  :6) ] obtenus sont tous situés au même endroit sur le cercle trigonométrique et ont donc tous même sinus et même cosinus.
:6) ] obtenus sont tous situés au même endroit sur le cercle trigonométrique et ont donc tous même sinus et même cosinus.Si on fait une vérification :
a = 2
 /3, cos a = -(1/2) et sin a = (
/3, cos a = -(1/2) et sin a = (  3)/2
3)/2si on prend b = -(
 /6) par exemple : cos b = (
/6) par exemple : cos b = (  3)/2 et sin b = -(1/2)
3)/2 et sin b = -(1/2) On voit bien que cos a = sin b et sin a = cos b.
Je crois que c'est fini,
j'espère que cela vous aidera
bonne journée.
mi_li_mi
mi_li_mi- Membre

-
 Nombre de messages : 11
Nombre de messages : 11
Age : 64
Localisation : France
Profession / Etudes : Maths-Physique
Points : 4833
Date d'inscription : 28/11/2011
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
» Devoir maison sur équilibre et réaction chimique
» Ma présentation
» projet scientique sur la LUMIERE
» La trajectoire de la Terre
» Equilibrer une réaction redox
» les effets sur les lignes de transport de l’électricité
» lignes de transport de l'électricité
» Gravitation
» Maquette suspension de moto 2D