Racine de 2 / Fractions continues ascendantes
3 participants
Page 1 sur 1
 Racine de 2 / Fractions continues ascendantes
Racine de 2 / Fractions continues ascendantes
Bonjour !
Peut on m'expliquer simplement comment on arrive à retrouver la fraction ascendante de :sqrt:2 ? (notamment pour le signe "moins" qui apparait de je ne sais trop où)
Et comment démontrer que les nombres sous les fractions résultent d'une suite? (du bas, vers le haut de la fraction continue ascendante)
Peut on m'expliquer simplement comment on arrive à retrouver la fraction ascendante de :sqrt:2 ? (notamment pour le signe "moins" qui apparait de je ne sais trop où)
Et comment démontrer que les nombres sous les fractions résultent d'une suite? (du bas, vers le haut de la fraction continue ascendante)

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Tu parles de ça :  ?
?
 ?
?- Spoiler:
- 1+\frac{1}{2+\frac{1}{2+...}}

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Non, cette fraction continue je pense l'avoir comprise: je parle des fractions continues ascendantes qui placent les barres de fractions au numérateur:
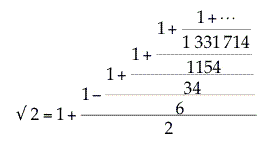
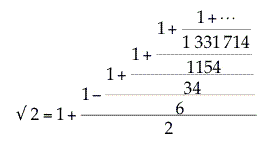

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Ah je ne connais pas ça ! Curieux d'en apprendre davantage à ce sujet...

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Moi aussi je suis curieuse d'en apprendre plus ^_^
Voilà le lien par lequel j'ai découvert cette notation de fraction continue ascendante
(il s'agit d'une conférence sur le nombre racine de 2):
http://www.cite-sciences.fr/francais/ala_cite/college/v2/html/2006_2007/conferences/conference_238.htm
Elle est expliquée dans la deuxième moitié de la vidéo il me semble. Donc si tu as compris tu pourrais me l'expliquer ? =D
Voilà le lien par lequel j'ai découvert cette notation de fraction continue ascendante
(il s'agit d'une conférence sur le nombre racine de 2):
http://www.cite-sciences.fr/francais/ala_cite/college/v2/html/2006_2007/conferences/conference_238.htm
Elle est expliquée dans la deuxième moitié de la vidéo il me semble. Donc si tu as compris tu pourrais me l'expliquer ? =D

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Arf... je ne peux pas lire la vidéo là...

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Parce que je suis sur Linux là et qu'il ne reconnaît pas le format de la vidéo.

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Sinon personne à part Julien ne s'intéresse à cette méthode de calcul? 
En tous cas, toute explication de la fraction continue ascendante de racine de 2 est la bien venue (même si ça n'est qu'un début d'explication, je le dévorerai volontiers)
(même si ça n'est qu'un début d'explication, je le dévorerai volontiers)
En tous cas, toute explication de la fraction continue ascendante de racine de 2 est la bien venue

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
J'ai jamais vu ça avant...

Duche- Modérateur

-
 Nombre de messages : 2210
Nombre de messages : 2210
Age : 39
Localisation : Louvain-la-Neuve (Belgique)
Profession / Etudes : Développeur en optimisation
Points : 8478
Date d'inscription : 16/01/2006
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Trop la flemme de redémarrer sur Win$$... mais à l'occasion, je regarderai !

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Alors, pour trouver le prochain numérateur, il te suffit de calculer le carré du dernier dénominateur (le plus haut) et de lui retrancher 2. Ca c'est l'algorithme pour calculer les numérateurs. Après, pour l'histoire du signe moins, apparemment, c'est assez compliqué (question ouverte). Sinon, pour ce qui est de la démonstration de la suite des numérateurs, je ne vois pas trop ce que tu demandes...

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
^_^ c gentil d'avoir regardé la conférence:
bah en faite d'où sort le premier nombre du dénominateur? comment est-on arrivé logiquement (ou géométriquement) à constater qu'il faut suivre cet algorithme? (parce qu'il ne l'ont pas pondu comme ça par un coup de génie ^_^) . Tu sais un peu comme ça a été expliqué pour la fraction continue si tu t'en rappelles...
bah en faite d'où sort le premier nombre du dénominateur? comment est-on arrivé logiquement (ou géométriquement) à constater qu'il faut suivre cet algorithme? (parce qu'il ne l'ont pas pondu comme ça par un coup de génie ^_^) . Tu sais un peu comme ça a été expliqué pour la fraction continue si tu t'en rappelles...

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Oui d'accord, je vois mieux ce que tu veux savoir... mais je n'en sais pas plus que toi ! Il développe bien le cas pour les fractions continues mais par pour le cas des fractions continues ascendantes ! Et le "moins" du départ est intriguant aussi.

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
En tous cas je suis super contente que tu te sois intéressé à la question! Je te remercie aussi pour ça ^_^

C-line- Membre

-
 Nombre de messages : 531
Nombre de messages : 531
Age : 34
Localisation : Amas de la Vierge
Profession / Etudes : Carpe diem
Points : 6637
Date d'inscription : 06/04/2008
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Avec plaisir, elle est intéressante cette conférence !

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: Racine de 2 / Fractions continues ascendantes
Re: Racine de 2 / Fractions continues ascendantes
Bonjour(ou plutot bonsoir), la fraction ascendante que tu décris ressemble à un développement en série de Engel (cf wikipédia pour l'algo) mais le (1-) du début est très très louche, il semble etrange qu'il y ait dans ta fraction ascendante que des (1+) sauf un seul (1-)...
a+
PS: les fractions continues sont assez amusantes, comme les radicaux imbriqués et les puissances itérées.
a+
PS: les fractions continues sont assez amusantes, comme les radicaux imbriqués et les puissances itérées.
Nabla- Invité
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
» Devoir maison sur équilibre et réaction chimique
» Ma présentation
» projet scientique sur la LUMIERE
» La trajectoire de la Terre
» Equilibrer une réaction redox
» les effets sur les lignes de transport de l’électricité
» lignes de transport de l'électricité
» Gravitation
» Maquette suspension de moto 2D