etudier le sens de variation de uv
2 participants
Page 1 sur 1
 etudier le sens de variation de uv
etudier le sens de variation de uv
bonjour a tous
j'ai un petit probleme sur exercice de maths auquel je ne comprends rien de rien
le voici:
1. Démontrer que si u et v sont croissantes sur un intervalle I et si pour tout réel x de I, u(x) 0 et v(x)
0 et v(x) 0, alors uv est croissante sur I
0, alors uv est croissante sur I
2. Dans chacun des cas suivants, la fonction uv est monotone sur I. Démontrer cette affirmation.
a) u et v sont croissantes sur I et pour tout réel x de I,
u(x) 0 et v(x)
0 et v(x) 0
0
b) u est croissante sur I, v est décroissante sur I et pour tout réel x de I,
u(x) 0 et v(x)
0 et v(x) 0
0
Je vous remercie d'avance de votre soutien.
J'ai un autre exercice a faire aussi mais je veux y réfléchir encore un peu avant de le mettre sur ce forum. Mais celui sur lequel je bloque pour l'instant, est a faire pour lundi.
j'ai un petit probleme sur exercice de maths auquel je ne comprends rien de rien
le voici:
1. Démontrer que si u et v sont croissantes sur un intervalle I et si pour tout réel x de I, u(x)
 0 et v(x)
0 et v(x) 0, alors uv est croissante sur I
0, alors uv est croissante sur I2. Dans chacun des cas suivants, la fonction uv est monotone sur I. Démontrer cette affirmation.
a) u et v sont croissantes sur I et pour tout réel x de I,
u(x)
 0 et v(x)
0 et v(x) 0
0b) u est croissante sur I, v est décroissante sur I et pour tout réel x de I,
u(x)
 0 et v(x)
0 et v(x) 0
0Je vous remercie d'avance de votre soutien.
J'ai un autre exercice a faire aussi mais je veux y réfléchir encore un peu avant de le mettre sur ce forum. Mais celui sur lequel je bloque pour l'instant, est a faire pour lundi.
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Bonjour,
pour la première question, u est croissante sur I donc si x1 x2, u(x1)
x2, u(x1)  u(x2).
u(x2).
De même pour v : v(x1) v(x2).
v(x2).
Or pout tout x de I, u et v sont positives donc on peut multiplier les 2 inégalités entre elles sans problème :
donc si x1 x2, u(x1) * v(x1)
x2, u(x1) * v(x1)  u(x2) * v(x2) soit encore uv(x1)
u(x2) * v(x2) soit encore uv(x1)  uv(x2).
uv(x2).
Donc uv est croissante sur I.
Est-ce-que tu es d'accord avec moi ?
pour la première question, u est croissante sur I donc si x1
 x2, u(x1)
x2, u(x1)  u(x2).
u(x2).De même pour v : v(x1)
 v(x2).
v(x2).Or pout tout x de I, u et v sont positives donc on peut multiplier les 2 inégalités entre elles sans problème :
donc si x1
 x2, u(x1) * v(x1)
x2, u(x1) * v(x1)  u(x2) * v(x2) soit encore uv(x1)
u(x2) * v(x2) soit encore uv(x1)  uv(x2).
uv(x2).Donc uv est croissante sur I.
Est-ce-que tu es d'accord avec moi ?

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 etudier le sens de variation de uv
etudier le sens de variation de uv
bonjour
je suis d'accord avec vous
merci
De plus, je suis vrament désolé et j'espere que vous ne l'avez pas encore cherché mais j'ai fait une petite faute en recopiant l'énoncé u 2. b)
voici le bon énoncé :
b) u est croissante sur I, v est décroissante sur I et pour tout réel x de I,
u(x) 0 et v(x)
0 et v(x) 0
0
je suis d'accord avec vous
merci
De plus, je suis vrament désolé et j'espere que vous ne l'avez pas encore cherché mais j'ai fait une petite faute en recopiant l'énoncé u 2. b)
voici le bon énoncé :
b) u est croissante sur I, v est décroissante sur I et pour tout réel x de I,
u(x)
 0 et v(x)
0 et v(x) 0
0
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Non je n'ai pas cherché la deuxième question encore. Mais avec la réponse à la première question, ça ne t'aide pas à pourquivre ?

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 etudier le sens de variation de uv
etudier le sens de variation de uv
bonjour,
ben en fait non je n'y arrive pas plus pour le 2. voulez vous bien me montrer peut etre que le 2.a pour l'instant
et puis l'autre exercice que j'ai essayé de faire mais ou je n'ai pas réussi non plu est le suivant :
une inégalité étrange
a) Etudier le sens de variation de la fonction x:tend: x+1/x sur ]0;+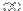 [
[
b) a,b,c,d,e,f,g,h, sont huit réels strictement positifs.
Démontrer l'inégalité:
a/h + h/a + b/g + g/b + c/f + f/c +d/e +e/d 8
8
mon prof m'a donné comme indication que :
a et b sont deux réels appartenant a ]0;+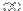 [
[
a:linf: b
f(a)-f(b)= a + 1/a - b -1/b
= a - b + 1/a -1/b
= a - b + (b-a)/(ab)
= (a - b)(1 - 1/ab)
= (a - b)[(ab-1)/ab]
on sait que a - b est négatif
on sait que ab est positif
il faut donc étudier le signe de ab-1
mais la je ne sais pas quoi faire
j'ai tracé la courbe sur ma calculette
faut-il faire des suppositions ? si oui je ne sais pas comment faire
merci de votre aide
ben en fait non je n'y arrive pas plus pour le 2. voulez vous bien me montrer peut etre que le 2.a pour l'instant
et puis l'autre exercice que j'ai essayé de faire mais ou je n'ai pas réussi non plu est le suivant :
une inégalité étrange
a) Etudier le sens de variation de la fonction x:tend: x+1/x sur ]0;+
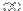 [
[b) a,b,c,d,e,f,g,h, sont huit réels strictement positifs.
Démontrer l'inégalité:
a/h + h/a + b/g + g/b + c/f + f/c +d/e +e/d
 8
8mon prof m'a donné comme indication que :
a et b sont deux réels appartenant a ]0;+
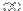 [
[ a:linf: b
f(a)-f(b)= a + 1/a - b -1/b
= a - b + 1/a -1/b
= a - b + (b-a)/(ab)
= (a - b)(1 - 1/ab)
= (a - b)[(ab-1)/ab]
on sait que a - b est négatif
on sait que ab est positif
il faut donc étudier le signe de ab-1
mais la je ne sais pas quoi faire
j'ai tracé la courbe sur ma calculette
faut-il faire des suppositions ? si oui je ne sais pas comment faire
merci de votre aide
en grand- Invité
 etudier le sens de variation de uv
etudier le sens de variation de uv
bonjour
excusez moi
je voudrais pas vous mettre la pression mais c'est pour demain.
merci
excusez moi
je voudrais pas vous mettre la pression mais c'est pour demain.
merci
en grand- Invité
 etudier le sens de variation de uv
etudier le sens de variation de uv
pour le 2.a du premier exercice
je pense avoir trouvé que si on multiplie par -1 -u(x) 0 et -v(x)
0 et -v(x) 0 on obtient a peu pres le meme énoncé que pour le 1., à savoir -u(x) et -v(x) positifs. donc on peut les multiplier entre eux.
0 on obtient a peu pres le meme énoncé que pour le 1., à savoir -u(x) et -v(x) positifs. donc on peut les multiplier entre eux.
est-ce bon?
je pense avoir trouvé que si on multiplie par -1 -u(x)
 0 et -v(x)
0 et -v(x) 0 on obtient a peu pres le meme énoncé que pour le 1., à savoir -u(x) et -v(x) positifs. donc on peut les multiplier entre eux.
0 on obtient a peu pres le meme énoncé que pour le 1., à savoir -u(x) et -v(x) positifs. donc on peut les multiplier entre eux.est-ce bon?
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Tu sais, c'est pas nous qui avons la pression !en grand a écrit:je voudrais pas vous mettre la pression mais c'est pour demain.
Je vais regarder en priorité ton nouvel exo... pour l'autre, tu dois être sur la bonne voie si tu as compris le 1).

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Bon, si tu as étudié le sens de variations de ta fonction, tu as sans doute remarqué qu'elle a un minimum qui est... ? Après, c'est fini !

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Quand tu as tracé ta fonction sur ta calculatrice, tu as vu qu'elle commençait par descendre puis qu'elle remontait...
Entre ces 2 instants, il y a donc un minimum ! A toi de le déterminer. T'es en quelle classe ?
Entre ces 2 instants, il y a donc un minimum ! A toi de le déterminer. T'es en quelle classe ?
Dernière édition par le Dim 21 Oct 2007 - 13:39, édité 1 fois

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Voilà !en grand a écrit:son minimum c'est 2 pour x=1 je pense
Maintenant, il faut t'en servir pour la suite ! C'est même pas la peine d'utiliser ce qu'a fait ton prof à mon avis...

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
D'accord.
Bon, si tu prends x=a/h avec ta première fonction, qu'est-ce-que tu obtiens comme inégalité ?
Bon, si tu prends x=a/h avec ta première fonction, qu'est-ce-que tu obtiens comme inégalité ?

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 etudier le sens de variation de uv
etudier le sens de variation de uv
oué mais pour le petit b je vois a peu pres ce qu'il faut faire mais comment peut-on savoir si les inconnus sont supérieurs pas à 1?
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Je ne vois pas où est ton problème. a et h étant strictement positifs, il en est de même pour a/h donc tu peux le rentrer dans la fonction initiale et en déduire l'inégalité intéressante.

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 etudier le sens de variation de uv
etudier le sens de variation de uv
pour x=a/h on obtient f(x)= a/h +h/a
et a chaque fois c'est pareil
mais on peut pas savoir si a/h:lsup: 1 ou si a/h:linf: 1
et a chaque fois c'est pareil
mais on peut pas savoir si a/h:lsup: 1 ou si a/h:linf: 1
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Oui, je suis d'accord.en grand a écrit:pour x=a/h on obtient f(x)= a/h +h/a
et a chaque fois c'est pareil
On n'en a pas besoin !en grand a écrit:mais on peut pas savoir si a/h:lsup: 1 ou si a/h:linf: 1
Tu sais que
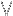 x
x  0, f(x)
0, f(x)  2 (car 2 est le minimum de la fonction sur ]0;+
2 (car 2 est le minimum de la fonction sur ]0;+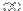 [ donc...
[ donc...
Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 etudier le sens de variation de uv
etudier le sens de variation de uv
il y a un truc que je ne sais pas: c'est ce que signifie ce signe 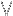
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Oui c'est normal !
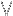 signifie "pour tout" ou "quel que soit"...
signifie "pour tout" ou "quel que soit"...
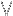 signifie "pour tout" ou "quel que soit"...
signifie "pour tout" ou "quel que soit"...
Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
C'est quoi 1ere chez vous? Au Luxembourg, c'est l'année du BAC...mais clairement ce n'est pas le cas chez vous sinon je me ferais des soucis :-). Julien, juste pour savoir: comment t'as su que le gars ne connaît pas les dérivées tout au départ quand il n'a rien dit sur son année d'études?

Sangoku- Membre

-
 Nombre de messages : 158
Nombre de messages : 158
Age : 40
Profession / Etudes : Etudiant en maths
Points : 6661
Date d'inscription : 05/09/2006
 etudier le sens de variation de uv
etudier le sens de variation de uv
ok merci
je voudrais savoir autre chose svp
pour en revenir au premier execice
si on a:
u et v sont croissantes sur I et pour tout réel x de I,
u(x) 0 et v(x)
0 et v(x) 0
0
est-ce que ca change le sens de variations si on fait
-u(x) 0 et -v(x)
0 et -v(x) 0 autrement dit en multipliant par -1
0 autrement dit en multipliant par -1
je voudrais savoir autre chose svp
pour en revenir au premier execice
si on a:
u et v sont croissantes sur I et pour tout réel x de I,
u(x)
 0 et v(x)
0 et v(x) 0
0est-ce que ca change le sens de variations si on fait
-u(x)
 0 et -v(x)
0 et -v(x) 0 autrement dit en multipliant par -1
0 autrement dit en multipliant par -1
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Bon même si tu connais pas, ceci peut t'aider pour mieux visualiser ton exo: note f(x) = u'(x)v(x)+u(x)v'(x) (dérivation). Ta fonction f(x) te donne toutes tes réponses. Que valent u'(x) et v'(x)? Et bien, si u (ou v) est croissant, u'(x)>=0 pour tout x. Et si u est décroissant, u(x) est inf ou égal à 0.
Ta question est dès lors évidente: u croiss -> u'>=0.
v croiss -> v' pos
Dès lors, f=u'v+v'u est nég dans ta question (donc uv est décroissant!), alors que ct pos (donc uv croissant) dans ton exemple de départ.
Tu vois?
Ta question est dès lors évidente: u croiss -> u'>=0.
v croiss -> v' pos
Dès lors, f=u'v+v'u est nég dans ta question (donc uv est décroissant!), alors que ct pos (donc uv croissant) dans ton exemple de départ.
Tu vois?

Sangoku- Membre

-
 Nombre de messages : 158
Nombre de messages : 158
Age : 40
Profession / Etudes : Etudiant en maths
Points : 6661
Date d'inscription : 05/09/2006
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
C'est un an avant le BAC...Sangoku a écrit:C'est quoi 1ere chez vous?
D'après le niveau du premier exo et parce qu'il n'avait pas compris quand je parlais du minimum... Quand on connaît les dérivées, ça va beaucoup plus vite !Julien, juste pour savoir: comment t'as su que le gars ne connaît pas
les dérivées tout au départ quand il n'a rien dit sur son année
d'études?

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Un an avant le bac??? Mais c'est là qu'on apprend les dérivées normalement non???

Sangoku- Membre

-
 Nombre de messages : 158
Nombre de messages : 158
Age : 40
Profession / Etudes : Etudiant en maths
Points : 6661
Date d'inscription : 05/09/2006
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Oui, c'est cette année qu'il va le découvrir, mais l'année vient de commencer !Sangoku a écrit:Un an avant le bac??? Mais c'est là qu'on apprend les dérivées normalement non???

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005
 etudier le sens de variation de uv
etudier le sens de variation de uv
c'est dans mon programme de cette année mais on en pas encore a ce chapitre
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Ok tu me rassures là.

Sangoku- Membre

-
 Nombre de messages : 158
Nombre de messages : 158
Age : 40
Profession / Etudes : Etudiant en maths
Points : 6661
Date d'inscription : 05/09/2006
 etudier le sens de variation de uv
etudier le sens de variation de uv
je tiens vraiment a encore vous remercier pour tout le temps que vous m'avez consacré.
bonne soirée
bonne soirée
en grand- Invité
 Re: etudier le sens de variation de uv
Re: etudier le sens de variation de uv
Avec plaisir.

Julien- Administrateur

-
 Nombre de messages : 12291
Nombre de messages : 12291
Age : 37
Localisation : Clermont-Ferrand
Profession / Etudes : Ingénieur
Points : 22712
Date d'inscription : 10/03/2005

Sangoku- Membre

-
 Nombre de messages : 158
Nombre de messages : 158
Age : 40
Profession / Etudes : Etudiant en maths
Points : 6661
Date d'inscription : 05/09/2006
 Sujets similaires
Sujets similaires» Etudier le sens de variation d'une fonction
» sens de variation de fonction U+V ayant un sens de variation contraire
» Etude du sens de variation d'une fonction u+v
» Etude du sens de variation d'une fonction
» Variation des fonction du type U+V
» sens de variation de fonction U+V ayant un sens de variation contraire
» Etude du sens de variation d'une fonction u+v
» Etude du sens de variation d'une fonction
» Variation des fonction du type U+V
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum
» Devoir maison sur équilibre et réaction chimique
» Ma présentation
» projet scientique sur la LUMIERE
» La trajectoire de la Terre
» Equilibrer une réaction redox
» les effets sur les lignes de transport de l’électricité
» lignes de transport de l'électricité
» Gravitation
» Maquette suspension de moto 2D